摘要:(1) .所以是周期为2的函数. (2)∵当x∈时, , ∴x∈[0,1]时, ∴当x∈时,. (3)由函数是以2为周期的函数.故只需要求出一个周期内的值域即可.由(2)知 .故在上函数的值域是.故值域为
网址:http://m.1010jiajiao.com/timu_id_3936759[举报]
设函数y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x)对一切x∈R都成立,又当x∈[-1,1]时,f(x)=x3,则下列五个命题:
①函数y=f(x)是以4为周期的周期函数;
②当x∈[1,3]时,f(x)=( x-2)3;
③直线x=±1是函数y=f(x)图象的对称轴;
④点(2,0)是函数y=f(x)图象的对称中心;
⑤函数y=f(x)在点(
,f(
))处的切线方程为3x-y-5=0.
其中正确的是
查看习题详情和答案>>
①函数y=f(x)是以4为周期的周期函数;
②当x∈[1,3]时,f(x)=( x-2)3;
③直线x=±1是函数y=f(x)图象的对称轴;
④点(2,0)是函数y=f(x)图象的对称中心;
⑤函数y=f(x)在点(
| 3 |
| 2 |
| 3 |
| 2 |
其中正确的是
①③
①③
.(写出所有正确命题的序号)
设函数y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x)对一切x∈R都成立,又当x∈[-1,1]时,f(x)=x3,则下列五个命题:
①函数y=f(x)是以4为周期的周期函数;
②当x∈[1,3]时,f(x)=( x-2)3;
③直线x=±1是函数y=f(x)图象的对称轴;
④点(2,0)是函数y=f(x)图象的对称中心;
⑤函数y=f(x)在点( ,f(
,f( ))处的切线方程为3x-y-5=0.
))处的切线方程为3x-y-5=0.
其中正确的是 .(写出所有正确命题的序号) 查看习题详情和答案>>
①函数y=f(x)是以4为周期的周期函数;
②当x∈[1,3]时,f(x)=( x-2)3;
③直线x=±1是函数y=f(x)图象的对称轴;
④点(2,0)是函数y=f(x)图象的对称中心;
⑤函数y=f(x)在点(
 ,f(
,f( ))处的切线方程为3x-y-5=0.
))处的切线方程为3x-y-5=0.其中正确的是 .(写出所有正确命题的序号) 查看习题详情和答案>>
设函数y=f(x)是定义在R上的奇函数,且f(x-2)=-f(x)对一切x∈R都成立,又当x∈[-1,1]时,f(x)=x3,则下列五个命题:
①函数y=f(x)是以4为周期的周期函数;
②当x∈[1,3]时,f(x)=( x-2)3;
③直线x=±1是函数y=f(x)图象的对称轴;
④点(2,0)是函数y=f(x)图象的对称中心;
⑤函数y=f(x)在点( ,f(
,f( ))处的切线方程为3x-y-5=0.
))处的切线方程为3x-y-5=0.
其中正确的是________.(写出所有正确命题的序号)
查看习题详情和答案>>
设函数y=f(x)是定义域为R的奇函数,且满足f(x-2)= -f(x)对一切x∈R恒成立,当x∈[0,1]时,
f(x)=x3,给出下列四个命题:
①f(x)是以4为周期的周期函数;
②f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③f(x)图象的对称轴有x=±1;
④f(x)在点(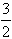 ,f(
,f(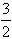 ))处的切线方程为3x+4y=5;
))处的切线方程为3x+4y=5;
⑤函数f(x)在R上无最大值。
其中正确命题的序号是( )(写出所有正确命题的序号)。
查看习题详情和答案>>
f(x)=x3,给出下列四个命题:
①f(x)是以4为周期的周期函数;
②f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③f(x)图象的对称轴有x=±1;
④f(x)在点(
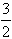 ,f(
,f(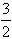 ))处的切线方程为3x+4y=5;
))处的切线方程为3x+4y=5;⑤函数f(x)在R上无最大值。
其中正确命题的序号是( )(写出所有正确命题的序号)。
(A类)定义在R上的函数y=f(x),对任意的a,b∈R,满足f(a+b)=f(a)•f(b),当x>0时,有f(x)>1,其中f(1)=2
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
.
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
<f(x)<m2+2km+k+
对一切实数x及m恒成立,求实数k的取值范围;
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
查看习题详情和答案>>
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
| -2x+b |
| 2x+1+a |
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
| 3 |
| 2 |
| 5 |
| 2 |
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.