摘要： 解:(Ⅰ)当a=1时.对函数求导数.得 -2分 令 列表讨论的变化情况: 3 + 0 - 0 + 极大值6 极小值-26 所以.的极大值是.极小值是 ------6分 (Ⅱ)的图像是一条开口向上的抛物线.关于x=a对称. 若上是增函数.从而 上的最小值是最大值是 由于是有 ----8分 由 ---10分 所以 若a>1,则不恒成立. 所以使恒成立的a的取值范围是 ------12分
网址：http://m.1010jiajiao.com/timu_id_3931037[举报]
已知函数
，其中实数a，b是常数．
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
查看习题详情和答案>>
已知函数f(x)=
x3-ax+b，其中实数a，b是常数．
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
查看习题详情和答案>>
| 1 |
| 3 |
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
已知函数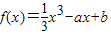
，其中实数a，b是常数．
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
查看习题详情和答案>>
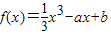，其中实数a，b是常数．（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
查看习题详情和答案>>
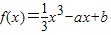，其中实数a，b是常数．
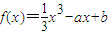，其中实数a，b是常数．