摘要: 设函数 (Ⅰ)证明其中为k为整数 (Ⅱ)设为的一个极值点.证明 (Ⅲ)设在内的全部极值点按从小到大的顺序排列为.证明: 2005年普通高等学校招生全国统一考试
网址:http://m.1010jiajiao.com/timu3_id_4469272[举报]
.(本小题满分14分)
设函数 .其中
.其中 为常数.
为常数.
(Ⅰ)证明:对任意 ,
, 的图象恒过定点;
的图象恒过定点;
(Ⅱ)
设 ,若
,若 为定义域
为定义域 上的增函数,求
上的增函数,求 的最大值;
的最大值;
(Ⅲ)当 时,函数
时,函数 是否存在极值?若存在,求出极值;若不存在,说明理由.
是否存在极值?若存在,求出极值;若不存在,说明理由.
查看习题详情和答案>>
本小题满分14分)
(Ⅰ)已知函数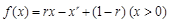 ,其中
,其中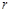 为有理数,且
为有理数,且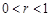 . 求
. 求 的最小值;
的最小值;
(Ⅱ)试用(Ⅰ)的结果证明如下命题:设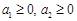 ,
,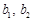 为正有理数. 若
为正有理数. 若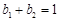 ,则
,则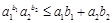 ;
;
(Ⅲ)请将(Ⅱ)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当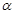 为正有理数时,有求导公式
为正有理数时,有求导公式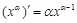 .
.
查看习题详情和答案>>
 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
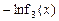 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.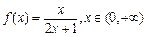 ,数列
,数列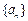 满足
满足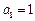 ,
,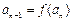 ;数列
;数列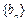 满足
满足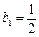 ,
,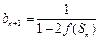 ,其中
,其中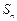 为数列
为数列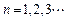
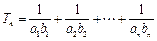 ,证明
,证明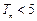 .
.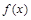 在
在 上有定义,对任意实数
上有定义,对任意实数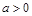 和任意实数
和任意实数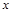 ,都有
,都有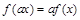 .
. 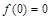 ;
;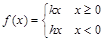 (其中k和h均为常数);
(其中k和h均为常数);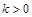 的时,设
的时,设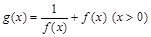 ,讨论
,讨论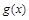 在
在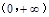 内的单调性.
内的单调性.