摘要: 设函数分别在.处取得极小值.极大值.平面上点A.B的坐标分别为.,该平面上动点P满足,点Q是点P关于直线的对称点.求(Ⅰ)点A.B的坐标 , (Ⅱ)动点Q的轨迹方程 18解: (Ⅰ)令解得 当时,, 当时, ,当时, 所以,函数在处取得极小值,在取得极大值,故, 所以, 点A.B的坐标为. (Ⅱ) 设.. .所以.又PQ的中点在上.所以 消去得
网址:http://m.1010jiajiao.com/timu3_id_4468873[举报]
(本小题满分14分) 已知函数![]()
(I)若![]() 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数![]() 的最小值;
的最小值;
(III)设函数![]() 的图象C1与函数
的图象C1与函数![]() 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(本小题满分14分) 已知函数![]()
(I)若![]() 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数![]() 的最小值;
的最小值;
(III)设函数![]() 的图象C1与函数
的图象C1与函数![]() 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(本小题满分14分)设函数![]() ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设![]() 、
、![]() 、
、![]() ,
,![]() 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求![]() 的方程;
的方程;
(Ⅱ)已知曲线G在点A![]() 、B
、B![]() 处的切线的斜率分别为0、
处的切线的斜率分别为0、![]() ,求证:
,求证:![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,当![]() 时,
时,![]() 恒成立,求常数
恒成立,求常数![]() 的最小值.
的最小值.
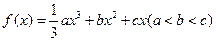 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设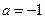 、
、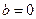 、
、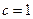 ,
,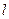 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求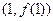 、B
、B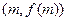 处的切线的斜率分别为0、
处的切线的斜率分别为0、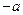 ,求证:
,求证: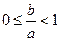 ;
;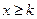 时,
时,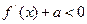 恒成立,求常数
恒成立,求常数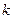 的最小值.
的最小值.
 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围; 的最小值;
的最小值; 的图象C1与函数
的图象C1与函数 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.