摘要: 函数在与上单调性相同.在与上单调性相反.当为何值时.取得极值?并判断出这些极值点的横坐标与2.4的大小关系,(3)的图象上是否存在点使f(x)在M处的切线斜率为?
网址:http://m.1010jiajiao.com/timu3_id_4468391[举报]
(本小题满分14分)如图,两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为 km,建在C处的垃圾处理厂对城A和城B的总影响度为
km,建在C处的垃圾处理厂对城A和城B的总影响度为 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(I)将 表示成
表示成 的函数;
的函数;
(II)讨论(1)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
查看习题详情和答案>>
(本小题满分14分)
已知函数 对任意实数
对任意实数 均有
均有 ,其中常数
,其中常数 为负数,且
为负数,且 在区间
在区间 上有表达式
上有表达式 .
.
(1)求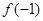 ,
, 的值;
的值;
(2)写出 在
在 上的表达式,并讨论函数
上的表达式,并讨论函数 在
在 上的单调性;
上的单调性;
(3)求出 在
在 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
查看习题详情和答案>>
(本小题满分14分)
已知函数 对任意实数
对任意实数 均有
均有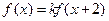 ,其中常数
,其中常数 为负数,且
为负数,且 在区间
在区间 上有表达式
上有表达式 .
.
(1)求 ,
, 的值;
的值;
(2)写出 在
在 上的表达式,并讨论函数
上的表达式,并讨论函数 在
在 上的单调性;
上的单调性;
(3)求出 在
在 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
 对任意实数
对任意实数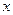 均有
均有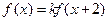 ,其中常数
,其中常数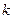 为负数,且
为负数,且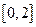 上有表达式
上有表达式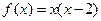 .
.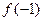 ,
,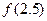 的值;
的值;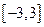 上的表达式,并讨论函数
上的表达式,并讨论函数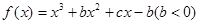 在[-1,0]和[0,2]上有相反的单调性.
在[-1,0]和[0,2]上有相反的单调性.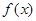 的图象上在两点
的图象上在两点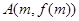 、
、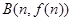 处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;
处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;