摘要：(三)性质:方程:, 焦点: .通径, 准线: , 焦半径:过焦点弦长 注意:(1)几何特征:焦点到顶点的距离=,焦点到准线的距离=,通径长= 顶点是焦点向准线所作垂线段中点. (2)抛物线上的动点可设为P或P
网址：http://m.1010jiajiao.com/timu3_id_4467938[举报]
如图，已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（1）已知椭圆C1：
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
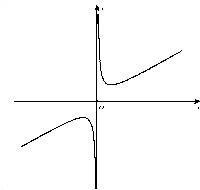已知等轴双曲线C的两个焦点F1、F2在直线y=x上，线段F1F2的中点是坐标原点，且双曲线经过点（3，| 3 |
| 2 |
（1）若已知下列所给的三个方程中有一个是等轴双曲线C的方程：①x2-y2=
| 27 |
| 4 |
| 9 |
| 2 |
（2）现要在等轴双曲线C上选一处P建一座码头，向A（3，3）、B（9，6）两地转运货物．经测算，从P到A、从P到B修建公路的费用都是每单位长度a万元，则码头应建在何处，才能使修建两条公路的总费用最低？
（3）如图，函数y=
| ||
| 3 |
| 1 |
| x |
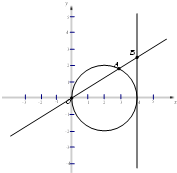（2011•南汇区二模）已知动直线y=kx交圆（x-2）2+y2=4于坐标原点O和点A，交直线x=4于点B，若动点M满足| OM |
| AB |
（1）试用k表示点A、点B的坐标；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）．
①对称性；（2分）
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；（2分）
③图形范围；（2分）
④渐近线；（3分）
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．（3分）
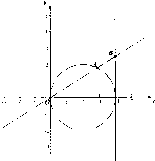已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足| OM |
| OB |
| OM |
| AB |
（1）试用点M的坐标x，y表示y0，x1，y1；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由．（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）
①对称性；
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；
③图形范围；
④渐近线；
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性． 查看习题详情和答案>>
（
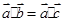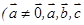为三个向量），则
”；
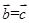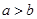，那么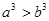
；
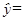1.5x+45，x∈{1,5,7,13,19}，则
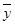=58.5；