摘要:已知定义域为的函数满足: ①时.,②,③对任意的正实数.都有 (Ⅰ)求证:, (Ⅱ)求证:在定义域内为减函数, (Ⅲ)求不等式的解集.
网址:http://m.1010jiajiao.com/timu3_id_4467302[举报]
已知定义域为![]() 的函数
的函数![]() 满足:①对任意
满足:①对任意![]() ,恒有
,恒有![]() 成立;当
成立;当![]() 时,
时,![]() 。给出如下结论:
。给出如下结论:
①对任意![]() ,有
,有![]() ;②函数
;②函数![]() 的值域为
的值域为![]() ;③存在
;③存在![]() ,使得
,使得![]() ;④“函数
;④“函数![]() 在区间
在区间![]() 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在![]() ,使得
,使得
![]() ”。
”。
其中所有正确结论的序号是 。
查看习题详情和答案>>已知定义域为![]() 的函数
的函数![]() 满足:①对任意
满足:①对任意![]() ,恒有
,恒有![]() 成立;当
成立;当![]() 时,
时,![]() 。给出如下结论:
。给出如下结论:
①对任意![]() ,有
,有![]() ;②函数
;②函数![]() 的值域为
的值域为![]() ;③存在
;③存在![]() ,使得
,使得![]() ;④“函数
;④“函数![]() 在区间
在区间![]() 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在![]() ,使得
,使得
![]() ”。
”。
其中所有正确结论的序号是 。
查看习题详情和答案>>已知定义域为 的函数
的函数 满足:(1)对任意
满足:(1)对任意 ,恒有
,恒有 成立;(2)当
成立;(2)当 时,
时, .给出如下结论:①对任意
.给出如下结论:①对任意 ,有
,有
 ;②函数
;②函数 的值域为
的值域为 ;③存在
;③存在 ,使得
,使得 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在 ,使得
,使得 ”.其中所有正确结论的序号是
.
”.其中所有正确结论的序号是
.
查看习题详情和答案>>
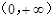 的函数
的函数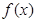 满足:①对任意
满足:①对任意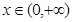 ,恒有
,恒有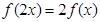 成立;当
成立;当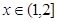 时,
时,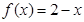 。给出如下结论:
。给出如下结论: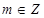 ,有
,有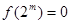 ;②函数
;②函数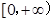 ;③存在
;③存在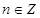 ,使得
,使得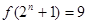 ;④“函数
;④“函数 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在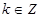 ,使得
,使得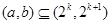 ”。其中所有正确结论的序号是
。
”。其中所有正确结论的序号是
。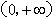 的函数
的函数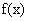 满足:①对任意
满足:①对任意 ,恒有
,恒有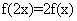 成立;当
成立;当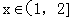 时,
时,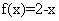 。给出如下结论:
。给出如下结论: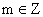 ,有
,有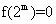 ;②函数
;②函数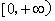 ;③存在
;③存在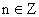 ,使得
,使得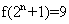 ;④“函数
;④“函数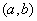 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在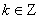 ,使得
,使得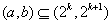 ”。
”。