摘要：11．分别把写有0.1.2.3.4数字的四张纸片放入一盒中.每次取一张记数字为m.放回后再取一张记数字为n.设P(m,n)为平面中的点.则点的概率为 A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_4465388[举报]
在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，…，这些数叫做三角形数，其通项为
，前n项和为sn=
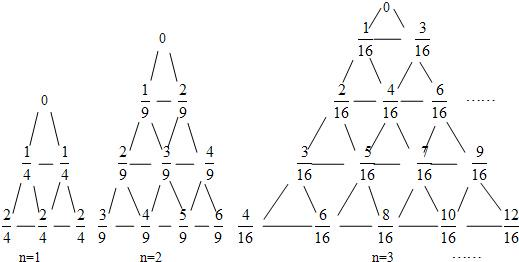
，如下图所示，有一列三角形数表，其位于三角形的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列，依次记各三角形数表中的所有数之和为an，则a1=
=
=2，a2=
=
=
．
（1）求a3，a4，并写出an的表达式；
（2）令bn=
+
，证明2n＜b1+b2+b3+…+bn＜2n+2（n∈N*）．
查看习题详情和答案>>
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
| 0+2+6 |
| 4 |
| 2(1+3) |
| 4 |
| 0+3+9+18 |
| 9 |
| 3(1+3+6) |
| 9 |
| 10 |
| 3 |
（1）求a3，a4，并写出an的表达式；
（2）令bn=
| an |
| an+1 |
| an+1 |
| an |
分别把写有0，1，2，3，4数字的四张纸片放入一盒中，每次取一张记数字为m，放回后再取一张记数字为n，设P（m,n）为平面中的点，则点P（m,n）∈{(x,y)|9x2+16y2≤144}的概率为( )
A.
B.
C.
D.
B.
C. 
D.
如图所示，正五边形ABCDE的每个顶点对应着一个整数，且这五个整数的和为正数．若其3个相邻顶点对应的整数依次为x、y、z，且y＜0，则要进行如下的操作：把整数x、y、z分别换为x+y，-y，z+y，称其为一次“求正”操作．只要五个整数中有负整数，“求正”操作就要继续进行．