摘要：已知:⑴p:两直线平行.q:斜率相等,⑵p:c=0.q:抛物线y=ax2+bx+c过原点,⑶p:ABS.q:.其中三组命题p是命题q的充要条件是---------------( ) (A)⑴.⑵ (B)⑵.⑶ (C)⑴.⑶ (D)⑵
网址：http://m.1010jiajiao.com/timu3_id_4464697[举报]
已知A、B是抛物线y2=4x上的相异两点．
（1）设过点A且斜率为-1的直线l1，与过点B且斜率为1的直线l2相交于点P（4，4），求直线AB的斜率；
（2）问题（1）的条件中出现了这样的几个要素：已知圆锥曲线Γ，过该圆锥曲线上的相异两点A、B所作的两条直线l1、l2相交于圆锥曲线Γ上一点；结论是关于直线AB的斜率的值．请你对问题（1）作适当推广，并给予解答；
（3）若线段AB（不平行于y轴）的垂直平分线与x轴相交于点Q（x0，0）．若x0＞2，试用x0表示线段AB中点的横坐标．
查看习题详情和答案>>
已知点M在椭圆D：
+
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
=2
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
+
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
| QP |
| PF |
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
| 3x2 |
| a2 |
| 4y2 |
| b2 |
已知直线l1，l2分别与双曲线C：
的两条渐近线平行，又与x轴分别交M，N于两点，且满足|OM|2+|ON|2=8。
（1）求直线l1与l2的交点H的轨迹的方程；
（2）过点S（0，3）作斜率为k的直线l，并且l与轨迹E交于不同两点P，Q，点R与点P关于y轴对称，证明直线RQ经过一定点。
查看习题详情和答案>>
的两条渐近线平行，又与x轴分别交M，N于两点，且满足|OM|2+|ON|2=8。（1）求直线l1与l2的交点H的轨迹的方程；
（2）过点S（0，3）作斜率为k的直线l，并且l与轨迹E交于不同两点P，Q，点R与点P关于y轴对称，证明直线RQ经过一定点。
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
的正三角形．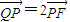
，求直线l的斜率；
左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．