摘要:=2= 17.解不等式:.
网址:http://m.1010jiajiao.com/timu3_id_4460994[举报]
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分
(1)已知矩阵M=
,β=
,(Ⅰ)求M-1;(Ⅱ)求矩阵M的特征值和对应的特征向量;(Ⅲ)计算M100β.
(2)曲线C的极坐标方程是ρ=1+cosθ,点A的极坐标是(2,0),求曲线C在它所在的平面内绕点A旋转一周而形成的图形的周长.
(3)已知a>0,求证:
-
≥a+
-2.
查看习题详情和答案>>
(1)已知矩阵M=
|
|
(2)曲线C的极坐标方程是ρ=1+cosθ,点A的极坐标是(2,0),求曲线C在它所在的平面内绕点A旋转一周而形成的图形的周长.
(3)已知a>0,求证:
a2+
|
| 2 |
| 1 |
| a |
(本题满分12分)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.

查看习题详情和答案>>
三.解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. (本题满分10分)
已知函数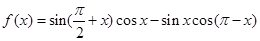 ,
,
(1)求函数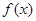 的最小正周期;
的最小正周期;
(2)在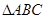 中,已知
中,已知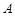 为锐角,
为锐角,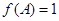 ,
,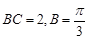 ,求
,求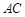 边的长.
边的长.
查看习题详情和答案>>
(本题满分共12分)某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温 差 | 10 | 13 | 11 | 12 | 7 |
| 感染数 | 23 | 32 | 24 | 29 | 17 |
(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为![]() 用
用![]() 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中![]() 视为同一事件,并求
视为同一事件,并求![]() 的事件A的概率。
的事件A的概率。