摘要: 关系分析法.即通过寻找关键词和关键量之间的数量关系的方法来建立问题的数学模型的方法. 例1. 某工厂有容量为300吨的水塔一个.每天从早上6时起到晚上10时止供应该厂生活和生产用水.已知该厂生活用水为每小时10吨.工业用水量W(吨)与时间(单位:小时.定义早上6时=0)的函数关系式为.水塔的进水量有10级.第一级每小时进水10吨.以后每提高一级.每小时的进水量增加10吨.若某天水塔原有水100吨.在供水同时打开进水管. (1)设进水量选用第级.写出在时刻水的存有量, (2)问进水量选择第几级.既能保证该厂用水又不会使水溢出. 读懂题目:题目涉及的关键词比较多:生活用水量.工业用水量.水的存有量.进水量.原有量.其数量关系为:存有量=进水量-用水量+原有量.而用水量=生活用水量+工业用水量.第一问的关键点是求“进水量选用第级 .第二问的关键点是“水塔中水不空不溢 转化为“存有量 . 建立数学模型:存有量=进水量-用水量+原有量.而用水量=生活用水量+工业用水量=10在选用第级的进水量时.时刻水的存有量为.要使水搭中水不空不溢.则.问题转化为确定.使.在()上恒成立. 求解数学模型:面对上述不等式.如何求解?是否会转化为“对一切恒成立. 是否会作一个代换“令 .将其转化为“对一切恒成立 .由于在上的最小值为在上的最大值为.从而确定.
网址:http://m.1010jiajiao.com/timu3_id_4460400[举报]
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:时)与当天投篮命中率y之间的关系:
用线性回归分析法,预测小李该月6号打6小时篮球的投篮命中率为
(参考公式:b=
,a=
-b
.参考数据:
(xi-
)(yi-
)=0.1,
(xi-
)2=10)
查看习题详情和答案>>
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
0.53
0.53
.(参考公式:b=
| |||||||
|
. |
| y |
. |
| x |
| 5 |
 |
| i=1 |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
. |
| x |
4、命题“在△ABC中,若∠C是直角,则∠B一定是锐角.”的证明过程如下:
假设∠B不是锐角,则∠B是直角或钝角,即∠B≥90°,
所以∠A+∠B+∠C≥∠A+90°+90°>180°,
这与三角形的内角和等于180°矛盾
所以上述假设不成立,所以∠B一定是锐角.
本题采用的证明方法是( )
假设∠B不是锐角,则∠B是直角或钝角,即∠B≥90°,
所以∠A+∠B+∠C≥∠A+90°+90°>180°,
这与三角形的内角和等于180°矛盾
所以上述假设不成立,所以∠B一定是锐角.
本题采用的证明方法是( )
查看习题详情和答案>>
23、课本小结与复习的参考例题中,给大家分别用“综合法”,“比较法”和“分析法”证明了不等式:已知a,b,c,d都是实数,且a2+b2=1,c2+d2=1,则|ac+bd|≤1.这就是著名的柯西(Cauchy.法国)不等式当n=2时的特例,即(ac+bd)2≤(a2+b2)(c2+d2),等号当且仅当ad=bc时成立.
请分别用中文语言和数学语言简洁地叙述柯西不等式,并用一种方法加以证明.
查看习题详情和答案>>
请分别用中文语言和数学语言简洁地叙述柯西不等式,并用一种方法加以证明.
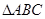 中,若
中,若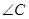 是直角,则
是直角,则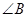 一定是锐角.”的证明过程如下:
一定是锐角.”的证明过程如下: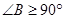 ,而
,而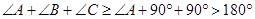 ,
,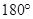 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立, ,只需证
,只需证 ,即需
,即需 ,即需证
,即需证 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了