摘要:20.(本题满分14分.第1小题满分6分.第二小题满分8分)已知函数f(x)=x+ x.数列|x|(x>0)的第一项x=1.以后各项按如下方式取定:曲线x=f(x)在处的切线与经过(0.0)和(x,f (x))两点的直线平行 . 求证:当n时. (Ⅰ)x (Ⅱ) 解:本题主要考查函数的导数.数列.不等式等基础知识.以及不等式的证明.同时考查逻辑推理能力. 证明:(I)因为 所以曲线在处的切线斜率 因为过和两点的直线斜率是 所以. (II)因为函数当时单调递增. 而 . 所以.即 因此 又因为 令 则 因为 所以 因此 故
网址:http://m.1010jiajiao.com/timu3_id_4456701[举报]
(本题满分14分,第1小题满分7分,第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用,将癌细胞注入一只小白鼠体内进行实验,经检测,癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.
|
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
癌细胞个数 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
… |
(1)要使小白鼠在实验中不死亡,第一次最迟应在第几天注射该种药物?(精确到1天)
(2)若在第10天,第20天,第30天,……给小白鼠注射这种药物,问第38天小白鼠是否仍然存活?请说明理由.
查看习题详情和答案>>
 ,
, ,
, 时,求
时,求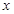 的值;
的值; 的最大值与最小值.
的最大值与最小值. ,
, ,
, 时,求
时,求 的值;
的值; 的最大值与最小值.
的最大值与最小值.

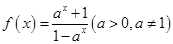 ,
,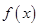 的反函数
的反函数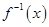 ;
;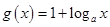 ,当
,当
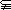
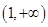 ,
,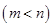 时,
时,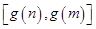 ,求
,求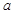 的取值范围.
的取值范围. ,
, 的反函数
的反函数 ;
; ,当
,当

 ,
, 时,
时, ,求
,求 的取值范围.
的取值范围.