如图所示,两个物体以相同大小的初速度从O点同时分别向x轴正、负方向水平抛出,它们的轨迹恰好满足抛物线方程y= ,那么以下说法正确的是(曲率半径简单地理解为在曲线上一点附近与之重合的圆弧的最大半径)
,那么以下说法正确的是(曲率半径简单地理解为在曲线上一点附近与之重合的圆弧的最大半径)
A.物体被抛出时的初速度为 |
B.物体被抛出时的初速度为 |
C.O点的曲率半径为 |
| D.O点的曲率半径为2k |
将一物体从空间某处水平抛出,在落地前1s内,它的速度与水平方向的夹角由30°变为60°,g取10m/s2不计空气阻力的影响,则下列说法不正确的( )
A.平抛运动的初速度为5 m/s m/s |
| B.从抛出经1.5s落地 |
| C.落地前1s内速度的变化量大小为10m/s,方向与落地时速度方向同向 |
| D.物体是从11.25m处下落的 |
玉树大地震,牵动了全国人民的心.一架装载救灾物资的直升飞机,以10 m/s的速度水平飞行,在距地面180 m的高度处,欲将救灾物资准确投放至地面目标,若不计空气阻力,g取10 m/s2,则
| A.物资投出后经过6 s到达地面目标 |
| B.物资投出后经过18 s到达地面目标 |
| C.应在距地面目标水平距离60 m处投出物资 |
| D.应在距地面目标水平距离180 m处投出物资 |
某人站在三楼阳台上,同时以10m/s的速率抛出两个小球,其中一个球竖直上抛,另一个球竖直下抛,它们落地的时间差为 ;如果该人站在六楼阳台上,以同样的方式抛出两个小球,它们落地的时间差为
;如果该人站在六楼阳台上,以同样的方式抛出两个小球,它们落地的时间差为 .不计空气阻力,
.不计空气阻力, 和
和 相比较,有
相比较,有
A. | B. | C. | D.无法判断 |
在一次救灾活动中,从水平飞行的直升机上投掷救灾物资。设飞机水平飞行的速度为v0,离地面高度为h,则当物资的速度方向与水平方向成θ时,物资的水平位移x与竖直位移y的关系为(不计空气阻力)
| A.x=ytanθ |
| B.x=2ytanθ |
C.x=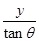 |
D.x=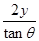 |
甲、乙两球位于同一竖直直线上的不同位置,甲比乙高出h。分别将甲、乙两球以v1、v2的速度沿同一水平方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
A.同时抛出,且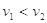 |
B.甲迟抛出,且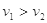 |
C.甲早抛出,且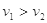 |
D.甲早抛出,且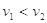 |
下面说法中正确的是 ( )
| A.物体做曲线运动时不一定有加速度 |
| B.平抛运动是匀变速运动,任意相等时间内速度的变化都相同 |
| C.匀速圆周运动虽然不是匀变速运动,但任意相等时间内速度的变化仍相同 |
| D.当物体受到的合外力为零时,物体仍然可以做曲线运动 |
如图所示,一网球运动员将球在边界处正上方水平向右击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法中正确的是:
| A.击球点高度h1与球网高度h2之间的关系为h1 =1.8h2 |
B.若保持击球高度不变,球的初速度υ0只要不大于 ,一定落在对方界内 ,一定落在对方界内 |
| C.任意降低击球高度(仍大于h2),只要击球初速度合适,球一定能落在对方界内 |
| D.任意增加击球高度,只要击球初速度合适,球一定能落在对方界内。 |
如图所示,光滑斜面固定在水平面上,顶端O有一小球,从静止释放,运动到底端B的时间是 ,若给小球不同的水平初速度,落到斜面上的A点,经过的时间是
,若给小球不同的水平初速度,落到斜面上的A点,经过的时间是 ,落到斜面底端B点,经过的时间是
,落到斜面底端B点,经过的时间是 ,落到水平面上的C点,经过的时间是
,落到水平面上的C点,经过的时间是 ,则( )
,则( )
A. | B.t2 > t3 | C. | D. |
如图所示,从倾角为θ的斜面上的M点水平抛出一个小球. 小球的初速度为 ,最后小球落在斜面上的N点,且重力加速度为g, 由上述条件某同学试图求出:①小球什么时刻与斜面间的距离最大;②小球空中运动的时间;③M、N之间的距离;④小球落到N点时的速度大小和方向等4个量。那么你认为他最多可以求出其中的( )
,最后小球落在斜面上的N点,且重力加速度为g, 由上述条件某同学试图求出:①小球什么时刻与斜面间的距离最大;②小球空中运动的时间;③M、N之间的距离;④小球落到N点时的速度大小和方向等4个量。那么你认为他最多可以求出其中的( )
| A.1个 | B.2个 | C.3个 | D.4个 |