如图所示,在光滑的水平面上有甲、乙两个木块,质量分别为m1和m2,中间用一原长为L、劲度系数为k的轻弹簧连接起来,现用一水平力F向左推木块乙,当两木块一起匀加速运动时,两木块之间的距离是
A. | B. | C. | D. |
质量为2kg的物体,只在两个力F1=2N、F2=10N的作用下,获得的加速度可能为( )
| A.3m/s2 | B.4m/s2 | C.5m/s2 | D.8m/s2 |
如图所示,三个物体质量分别为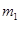 =1.0kg、
=1.0kg、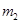 =2.0kg、
=2.0kg、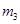 ="3.0kg" ,已知斜面上表面光滑,斜面倾角
="3.0kg" ,已知斜面上表面光滑,斜面倾角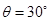 ,
,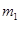 和
和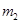 之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止,当撤掉外力时,
之间的动摩擦因数μ=0.8。不计绳和滑轮的质量和摩擦。初始用外力使整个系统静止,当撤掉外力时,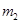 将(g=10m/s2,最大静摩擦力等于滑动摩擦力)
将(g=10m/s2,最大静摩擦力等于滑动摩擦力)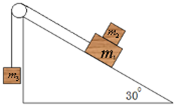
A.和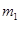 一起沿斜面下滑 一起沿斜面下滑 | B.和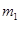 一起沿斜面上滑 一起沿斜面上滑 | C.相对于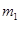 上滑 上滑 | D.相对于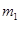 下滑 下滑 |
如图甲所示,用一水平力F拉着一个静止在倾角为(的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图像如图乙所示,g取10m/s2,根据图乙中所提供的信息可以计算出( )
| A.物体的质量 |
| B.斜面的倾角 |
| C.物体能静止在斜面上所施加的最小外力 |
| D.加速度为6 m/s2时物体的速度 |
放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t的关系如图所示.取重力加速度g=10m/s2.由此两图线可以求得物块的质量m和物
块与地面之间的动摩擦因数μ分别为( )
| A.m=0.5kg,μ=0.4 |
B.m=1.5kg,μ= |
| C.m=0.5kg,μ=0.2 |
| D.m=1kg, μ=0.2 |
小车上有一根固定的水平横杆,横杆左端固定的斜杆与竖直方向成θ角,斜杆下端连接一质量为m的小铁球。横杆右端用一根轻质细线悬挂一相同的小铁球,当小车在水平面上做直线运动时,细线保持与竖直方向成α角(α≠θ),设斜杆对小铁球的作用力为F,下列说法正确的是
A.F沿斜杆向上,F= |
B.F沿斜杆向上,F= |
C.F平行于细线向上,F= |
D.F平行于细线向上,F= |
a、b两物体的质量分别为m1、m2,由轻质弹簧相连。当用恒力F竖直向上拉着 a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1;当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2,如图所示。则
| A.x1一定等于x2 |
| B.x1一定大于x2 |
| C.若m1>m2,则 x1>x2 |
| D.若m1<m2,则 x1<x2 |
 ,在t=5s的时间内滑下的路程s=60m,g取10m/s2,求:
,在t=5s的时间内滑下的路程s=60m,g取10m/s2,求:
 、
、 .在拉力F作用下,A和B以加速度
.在拉力F作用下,A和B以加速度 做匀加速直线运动.某时刻突然撤去拉力
做匀加速直线运动.某时刻突然撤去拉力 ,此瞬时A和B的加速度为
,此瞬时A和B的加速度为 、
、 ,则( )
,则( )
 B.
B. ;
;
 ;
; D.
D.


