不计空气阻力，以一定的初速度竖直上抛一物体，从抛出至回到抛出点的时间为t，现在物体上升的最大高度的一半处设置一块挡板，物体撞击挡板前后的速度大小相等、方向相反，撞击所需时间不计，则这种情况下物体上升和下降的总时间约为（ ）
| A．0.5t | B．0.4t | C．0.3t | D．0.2t |
图像可能正确的是
两个石子做竖直上抛运动，初速度大小之比为2:3，则它们上升的最大高度和到达最高点所用的时间之比分别为（ ）
| A．4:9 4:9 | B．2:3 2:3 | C．4:9 2:3 | D．2: 2:3 |
两体积相同的小石块和小纸团，在同一位置以相同的速度竖直向上抛出。在没有空气阻力的条件下，两物体从抛出到上升到最高点（速度为0）所用的时间分别为t1、t2。可以猜测：
| A．t1 ＝t2 | B．t1 ＞t2 | C．t1 ＜t2 | D．无法判断 |
由消防水龙带的喷嘴喷出水的流量是0.28m3/min，水离开喷口时的速度大小为16
m/s，方向与水平面夹角为60度，在最高处正好到达着火位置，忽略空气阻力，则空中水柱的高度和水量分别是（重力加速度g取10m/s2）
| A．28.8m，1.12×10-2m3 | B．28.8m，0.672m3 |
| C．38.4m，1.29×10-2m3 | D．38.4m，0.776m3 |
如图所示，将小球沿与水平方向成α角以速度v向右侧抛出，经时间t1击中墙上距水平面高度为h1的A点；再将此球仍从同一点以相同速率抛出，抛出速度与水平方向成β（β>α）角，经时间t2击中墙上距水平面高度为h2的B点（图中未标出），空气阻力不计，则
| A．t1一定小于t2 | B．t1一定大于t2 |
| C．h1一定小于h2 | D．h1一定大于h2 |
为了测量蹦床运动员从蹦床上跃起的高度，探究小组设计了如下的方法：他们在蹦床的弹性网上安装压力传感器，利用传感器记录运动员在运动过程中对弹性网的压力，来推测运动员跃起的高度。右图为某段时间内蹦床运动员的压力—时间图象。运动员在空中仅在竖直方向上运动，且可视为质点，则可估算出运动员在这段时间内跃起的最大高度为（g取10m/s2）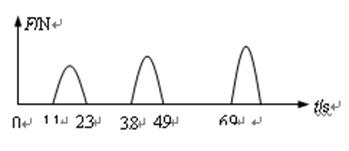
| A．1.5m | B．1. 8m |
| C．5.0m | D．7.2m |
一只气球以10 m/s的速度匀速上升，某时刻在气球正下方距气球6 m处有一小石子以20 m/s的初速度竖直上抛，若g取10 m/s2，不计空气阻力，则以下说法正确的是
| A．石子能追上气球，且在抛出后1s 时追上气球 |
| B．石子能追上气球，且在抛出后1.5s 时追上气球 |
| C．石子能追上气球，如果追上时不会发生碰撞且保持原运动状态，则石子能和气球相遇2次 |
| D．石子追不上气球 |
在距水平地面一定高度的某点，同时将两物体分别沿竖直方向与水平方向抛出（不计空气阻力），关于都落地的两物体下列说法正确的是：
| A．加速度相同 | B．机械能都守恒 |
| C．一定同时落地 | D．位移相同 |
一物体从某一行星表面竖直向上抛出(不计空气阻力).设抛出时t=0,得到物体上升高度随时间变化的h t图象如图所示,则该行星表面重力加速度大小与物体被抛出时的初速度大小分别为 （ ）
| A．8 m/s2, 20 m/s | B．10 m/s2, 25 m/s |
| C．8 m/s2, 25 m/s | D．10 m/s2, 20 m/s |