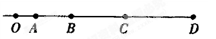做匀变速直线运动的物体,在时间t内的位移为 s ,设这段时间的中间时刻的瞬时速度为v1 ,这段位移的中间位置的瞬时速度为v2 ,则( )
| A.物体作匀加速运动时,v1> v2 |
| B.物体作匀加速运动时,v1< v2 |
| C.物体作匀减速运动时,v1> v2 |
| D.物体作匀减速运动时,v1< v2 |
一物体做匀加速直线运动,在第1个t s内位移为x1;第2个t s内位移为x2,则物体
在第1个t s末的速度是( )
| A.(x2-x1)/t | B.(x2+x1)/t | C.(x2-x1)/2t | D.(x2+x1)/2t |
不计重力的带电粒子在足够大的匀强电场中从A点静止释放,经过时间t,通过的路程为s,若此时突然使场强大小不变而方向相反,则带电粒子以后的运动情况是
| A.立即反向运动 |
| B.经过3t时间回到A点 |
C.经过 时间回到A点 时间回到A点 |
| D.从释放到回到A点时,总路程为4s |
如图所示.一个小物体沿光滑斜面由A点从静止开始加速下滑,在它通过的路径中取AE并分成相等的四段,VB表示通过B点时的瞬时速度,V表示AE段的平均速度.则VB与V的关系是 ( )
| A.VB<V | B.VB=V |
| C.VB>V | D.以上三种关系都有可能 |
汽车以10m/s的速度在平直公路上行驶,急刹车时的加速度大小为2m/s2,则自刹车开始,2s与6s时汽车的位移之比为( )
| A.16∶25 | B.16∶24 | C.25∶16 | D.16∶23 |
物体第1s由静止向东做加速度为1m/s2的匀加速直线运动,第2s加速度方向向西,大小不变,以后每隔1s加速度的方向都改变一次,但大小不变,如此反复只改变加速度的方向,共历时1 min。则在此1min内( )
| A.物体时而向东运动,时而向西运动,在1 min 末静止于初始位置之西 |
| B.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东30m的位置 |
| C.物体时而向东运动,时而向西运动,在1 min 末继续向东运动 |
| D.物体一直向东运动,从不向西运动,在1 min 末静止于初始位置之东15m的位置 |
一辆汽车从静止开始匀加速开出,然后保持匀速运动,最后匀减速运动直到停止。从汽车开始运动起计时,下表给出了某些时刻汽车的瞬时速度。根据表中的数据通过分析、计算可以得出( )
| 时刻(s) | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
| 速度(m/s) | 3.0 | 6.0 | 9.0 | 12 | 12 | 9.0 | 3.0 |
B.汽车匀速运动的时间为5s
C.汽车减速运动的加速度大小为6m/s2
D.汽车减速运动的时间为1.5s