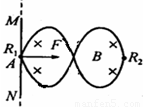
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,重力加速度g取l0m/s2.试求
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,重力加速度g取l0m/s2.试求| 时间t(s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 下滑距离s(m) | 0.1 | 0.3 | 0.7 | 1.4 | 2.1 | 2.8 | 3.5 |
(2)金属棒ab在开始运动的0.7s内,电阻R上产生的热量;
(3)从开始运动到t=0.4s的时间内,通过金属棒ab的电量.
 kx2,不计空气阻力和其他电阻,求:
kx2,不计空气阻力和其他电阻,求:

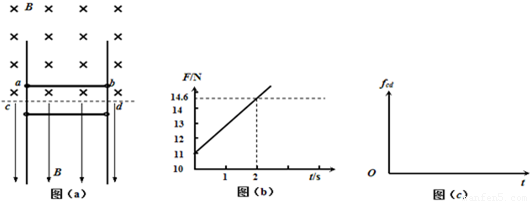
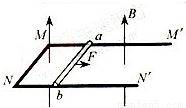
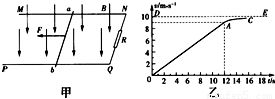
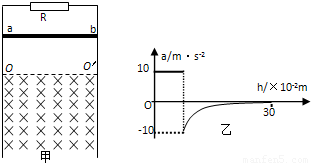 如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求:
如图甲所示,两条足够长的光滑平行金属导轨竖直放置,导轨问距为L=1m,两导轨的,上端间接有电阻,阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场,磁场磁感应强度为2T,现将质量m=0.1kg电阻不计的金届杆ab,从OO′上方某处由静止释放,金属杆在下落的过程中与导轨保持良好接触,且始终保持水平,不计导轨的电阻.已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示.求: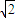 sin
sin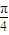 x m.求:
x m.求: