在沿水平方向的匀强磁场中,有一圆形金属圈可绕沿其直径的竖直轴自由转动,开始时线圈静止,线圈平面与磁场方向既不平行也不垂直,所成的锐角为 。在磁场开始增强后的一个极短时间内,线圈平面( )
。在磁场开始增强后的一个极短时间内,线圈平面( )
| A.维持不动 |
B.将向使 减小的方向转动 减小的方向转动 |
C.将向使 增大的方向转动 增大的方向转动 |
D.将转动,因不知磁场方向,不能确定 会增大还是会减小 会增大还是会减小 |
如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒下落距离为0.2R时铜棒中电动势大小为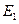 ,下落距离为0.8R时电动势大小为
,下落距离为0.8R时电动势大小为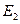 ,忽略涡流损耗和边缘效应.关于
,忽略涡流损耗和边缘效应.关于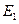 、
、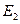 的大小和铜棒离开磁场前两端的极性,下列判断正确的是( )
的大小和铜棒离开磁场前两端的极性,下列判断正确的是( )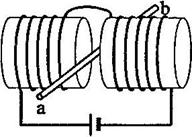
A.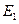 > >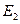 ,a端为正 ,a端为正 | B.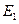 > >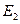 ,b端为正 ,b端为正 |
C.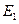 < <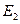 ,a端为正 ,a端为正 | D.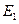 < < ,b端为正 ,b端为正 |
如图,在口字形闭合铁芯上绕有一组线圈,与滑动变阻器、电池构成闭合回路。a、b、c为三个闭合金属环,假定线圈产生的磁场全部集中在铁芯内,在滑动变阻器的滑片左右滑动时,能够产生感应电流的圆环是
| A.a、b两环 | B.b、c两环 |
| C.a、c两环 | D.a、b、c三环 |
如图所示,电阻不计的平行金属导轨固定在一绝缘斜面上,两相同的金属导体棒a、b垂直于导轨静止放置,且与导轨接触良好,匀强磁场垂直穿过导轨平面。现用一平行于导轨的恒力F作用在a的中点,使其向上运动。若b始终保持静止,则它所受摩擦力可能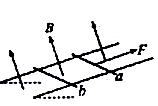
| A.变为0 | B.先减小后不变 |
| C.等于F | D.先增大再减小 |
法拉第通过设计的一系列试验,发现了电磁感应定律,并把历史上人们一直认为各自独立的两个学科“电学”与“磁学”联系在一起了。在下面给出的几个典型实验设计思想中,推论被后来的实验否定了的是 ( )
| A.既然磁铁可使近旁的铁块带磁,静电荷可使近旁的导体表面感应出电荷,那么静止导线上的稳恒电流也可在近旁静止的线圈中感应出电流 |
| B.既然磁铁可在近旁运动的导体中感应出电动势,那么稳恒电流也可在近旁运动的线圈中感应出电流 |
| C.既然运动的磁铁可在近旁静止的线圈中感应出电流,那么静止的磁铁也可在近旁运动的导体中感应出电动势 |
| D.既然运动的磁铁可在近旁的导体中感应出电动势,那么运动导线上的稳恒电流也可在近旁的线圈中感应出电流 |
两块水平放置的金属板间的距离为d,用导线与一个多匝线圈相连,线圈电阻为r,线圈中有竖直方向均匀变化的磁场,其磁通量的变化率为k,电阻R与金属板连接,如图所示。两板间有一个质量为m,电荷量为+q的油滴恰好处于静止状态,重力加速度为g,则线圈中的磁感应强度B的变化情况和线圈的匝数n分别为( )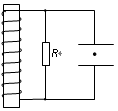
A.磁感应强度B竖直向上且正在增强,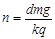 |
B.磁感应强度B竖直向下且正在增强,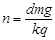 |
C.磁感应强度B竖直向上且正在减弱,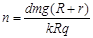 |
D.磁感应强度B竖直向下且正在减弱,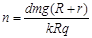 |
如图所示的是一个水平放置的玻璃环形小槽,槽内光滑、槽的宽度和深度处处相同.现将一直径略小于槽宽的带正电的小球放入槽内,让小球获一初速度v0在槽内开始运动,与此同时,有一变化的磁场竖直向下穿过小槽外径所包围的面积,磁感应强度的大小随时间成正比增大,设小球运动过程中带电量不变,那么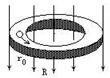
| A.小球受到的向心力大小不变 |
| B.小球受到的向心力大小增加 |
| C.磁场力对小球做功 |
| D.小球受到的磁场力不断增加 |
根据麦克斯韦电磁场理论,如下说法正确的是:( )
| A.变化的电场一定产生变化的磁场 |
| B.均匀变化的电场一定产生均匀变化的磁场 |
| C.稳定的电场一定产生稳定的磁场 |
| D.周期性变化的电场一定产生周期性变化的磁场 |
两根足够长的光滑导轨竖直放置,间距为L,底端接阻值为R的电阻。将质量为m,电阻也为R的金属棒悬挂在一个固定的轻弹簧下端,金属棒与导轨接触良好,导轨所在的平面与磁感应强度为B的磁场垂直,如图所示。除金属棒和电阻R外,其余电阻不计。现将金属棒从弹簧的原长位置由静止释放,则: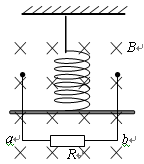
| A.金属棒向下运动时,流过电阻R的电流方向为b→a |
| B.最终弹簧的弹力与金属棒的重力平衡 |
C.金属棒的速度为v时,所受的安培力大小为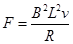 |
D.金属棒的速度为v时,金属棒两端的电势差为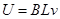 |
 处于方向竖直向下的匀强磁场中,金属杆
处于方向竖直向下的匀强磁场中,金属杆 与金属框架接触良好。在两根导轨的端点d、e之间连接一个电阻置,其他部分电阻忽略不计。现用一水平向右的外力F作用在金属杆
与金属框架接触良好。在两根导轨的端点d、e之间连接一个电阻置,其他部分电阻忽略不计。现用一水平向右的外力F作用在金属杆 图像,则下图中可以表示外力F随时间
图像,则下图中可以表示外力F随时间 变化关系的图像是 ( )
变化关系的图像是 ( )