模块3-5试题
(1)下列说法中正确的是
| A.玻尔的三个假设成功的解释了氢原子发光现象 |
B.卢瑟福在 粒子散射实验中发现了电子 粒子散射实验中发现了电子 |
| C.居里夫人在原子核人工转变的实验中发现了中子 |
| D.爱因斯坦为解释光电效应的实验规律提出了光子说 |
 粒子与一个静止于磁感应强度为B的匀强磁场中某点的氮核(
粒子与一个静止于磁感应强度为B的匀强磁场中某点的氮核( )发生正碰。碰后产生两个新核,在磁场中形成如图14所示的两条半径分别为R和r (R>r)的圆形径迹。其中R是质量较小核的经迹,r是质量较大核的经迹。
)发生正碰。碰后产生两个新核,在磁场中形成如图14所示的两条半径分别为R和r (R>r)的圆形径迹。其中R是质量较小核的经迹,r是质量较大核的经迹。①请写出该核反应方程;
②求出碰前
 粒子的速度(质子质量为m,电量为e)。
粒子的速度(质子质量为m,电量为e)。
 ,不计电子所受重力。
,不计电子所受重力。


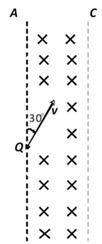
 g、带电量为q=5×10-6C的正粒子,并使之以v=10m/s的速度垂直于磁场方向开始运动,运动方向如图所示,不计粒子重力,磁场足够大。
g、带电量为q=5×10-6C的正粒子,并使之以v=10m/s的速度垂直于磁场方向开始运动,运动方向如图所示,不计粒子重力,磁场足够大。
 =108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求:
=108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求:
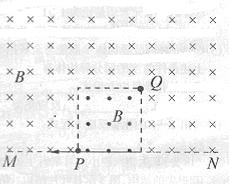

 m。已知粒子
m。已知粒子 能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求:
能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求: