物体在周期性驱动力作用下做受迫振动,固有频率为f1,驱动力的频率为f2,物体做受迫振动的频率为f,则
| A.f = f1 | B.f = f2 | C.f>f1 | D.f<f2 |
如图(甲)所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统。当圆盘静止时,小球可稳定振动。现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定。改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图(乙)所示,则
| A.此振动系统的固有频率约为3Hz |
| B.此振动系统的固有频率约为0.25Hz |
| C.若圆盘匀速转动的周期增大,系统的振动频率不变 |
| D.若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动 |
下列说法正确的是( )
| A.若声波波源向观察者靠近,则观察者接收到的声波频率减小 |
| B.声波击碎玻璃杯的实验原理是共振 |
| C.超声波在水中传播的距离要比光波和无线电波远得多 |
| D.“闻其声不见其人”是声波的干涉现象 |
一砝码和一轻弹簧构成弹簧振子,如图甲所示的装置可用于研究该弹簧振子的受迫振动.匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动.把手匀速转动的周期就是驱动力的周期,改变把手匀速动的速度就可以改变驱动力的周期.若保持把手不动,给砝码一向下的初速度,码砝便做简谐运动,振动图线如图乙所示. 当把手以某一速度匀速转动,受迫振动达到稳定时,砝码的振动图象如图丙所示.
若用T0表示弹簧振子的固有周期,T表示驱动力的周期,Y表示受迫振动达到稳定后砝码振动的振幅,则( )
| A.由图表可知T0="4" s |
| B.由图线可知T0="8" s |
| C.当T在4 s附近时,Y显著增大,当T比4 s小得多或大得多时,Y很小 |
| D.当T在8 s附近时,Y显著增大,当T比8 s小得多或大得多时,Y很小 |
正在运转的洗衣机,当脱水桶转得很快时,机身振动并不强烈,而切断电源,转动逐渐减慢直到停下来的过程中,在某一时刻t时,机身反而会发生强烈振动,此后脱水桶转速继续减慢,机身的振动也随之减弱,这种现象说明:
| A.纯属偶然现象,并无规律 |
| B.转动逐渐减慢过程中驱动力的频率不变 |
| C.转动逐渐减慢过程中洗衣机的固有频率不变 |
| D.t时刻脱水桶的惯性最大 |
一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则 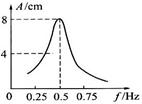
| A.此单摆的固有周期约为0.5s |
| B.此单摆的摆长约为2m |
| C.若摆长减小,单摆的固有频率增大 |
| D.若摆长增大,共振曲线的峰将向右移动 |
2011年3月11日14时46分,日本宫城县和岩手县等地发生9.0级地震,导致很多房屋坍塌,场景惨不忍睹,就此事件,下列说法正确的有
| A.所有建筑物都发生了共振 |
| B.所有建筑物振幅相同 |
| C.建筑物的振动周期由其固有周期决定 |
| D.所有建筑物均做受迫振动,且振动周期相同 |
如图所示是一个单摆在地球表面做受迫振动时的共振曲线,它表示振幅A与驱动力的频率f的关系,关于此单摆下列说法正确的是( )
| A.摆长约为10cm |
| B.摆长约为1m |
| C.若增大摆长,共振曲线的“峰”将向右移动 |
| D.若增大摆长,共振曲线的“峰”将向左移动 |
(2009年高考宁夏理综卷)某振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f.若驱动力的振幅保持不变,下列说法正确的是( )
| A.当f<f0时,该振动系统的振幅随f增大而减小 |
| B.当f>f0时,该振动系统的振幅随f增大而增大 |
| C.该振动系统的振动稳定后,振动的频率等于f0 |
| D.该振动系统的振动稳定后,振动的频率等于f |