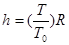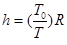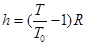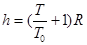图(1)是利用砂摆演示简谐运动图象的装置。当盛砂的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的砂在板上形成的曲线显示出砂摆的振动位移随时间变化的关系。第一次以速度v1匀速拉动木板,图(2)给出了砂摆振动的图线;第二次仅使砂摆的振幅减半,再以速度v2匀速拉动木板,图(3)给出了砂摆振动的图线。由此可知,砂摆两次振动的周期T1和T2以及拉动木板的速度v1和v2的关系是
| A.T1∶T2=2∶1 | B.T1∶T2=1∶2 |
| C.v1∶v2=1∶2 | D.v1∶v2=2∶1 |
如图5所示是一个单摆在地球表面做受迫振动时的共振曲线,它表示振幅A与驱动力的频率f的关系,关于此单摆下列说法正确的是( )
| A.摆长约为10cm |
| B.摆长约为1m |
| C.若增大摆长,共振曲线的“峰”将向右移动 |
| D.若增大摆长,共振曲线的“峰”将向左移动 |
一个摆长为L1的单摆,在地面上做简谐运动,周期为T1,已知地球质量为M1,半径为R1,另一摆长为L2的单摆,在质量为M2,半径为R2的星球表面做简谐运动,周期为T2,若T1=2T2,L1=4L2,M1=4M2,则地球半径与星球半径之比R1∶R2为
| A.2∶1 | B.2∶3 |
| C.1∶2 | D.3∶2 |
如图所示,虚线和实线分别为甲、乙两个弹簧振子做简谐运动的图象.已知甲、乙两个振子质量相等,则
| A.甲、乙两振子的频率相同 |
| B.甲、乙两个振子的相位差恒为π |
| C.前2秒内甲、乙两振子的加速度均为正值 |
| D.第2秒末甲的速度最大,乙的加速度最大 |
一座在地球上走时准确的摆钟,到某行星上后,分针走一圈经历的实际时间是3小时,已知该行星的半径是地球半径的1/4,则该行星上的第一宇宙速度应为地球上的第一宇宙速度的( )
| A.2/3 | B.3/2 | C.1/6 | D.6 |
如图,(a)为一波源的共振曲线,(b)图中的a表示该波源在共振状态下的振动形式沿x轴传播过程中形成的机械波在t=0时刻的波形曲线。则下列说法错误的是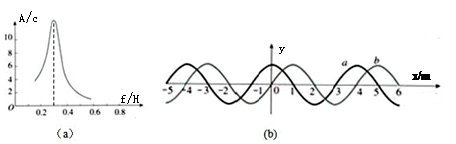
| A.(a)图中,若驱动力周期变小共振动曲线的峰将向频率f大的方向移动 |
| B.(b)图中,波速一定为1.2m/s |
| C.(b)图中,a、b波形时间间隔可能为2.5s |
| D.(b)图中,遇到宽度为2m的狭缝能发生明显的衍现象 |
如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘接在一起,且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后( )?
A.摆动的周期为 T T |
B.摆动的周期为 T? T? |
| C.摆球的最高点与最低点的高度差为0.3h |
| D.摆球的最高点与最低点的高度差为0.25h? |
一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则 ( )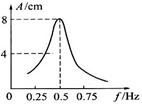
| A.此单摆的固有周期约为0.5s |
| B.此单摆的摆长约为2m |
| C.若摆长减小,单摆的固有频率增大 |
| D.若摆长增大,共振曲线的峰将向左移动 |

 B.
B. C.π
C.π D.2π
D.2π