某同学在用单摆测重加速度的实验中,用的摆球密度不均匀,无法确定重心位置,他第一次量得悬线长为L1(不计摆球半径),测得周期为T1,第二次量得悬线长为L2,测得周期为T2,根据上述数据,重力加速度g的值为:( )
A. | B. |
C. | D.无法判断 |
如图所示的MON是曲率半径很大的圆弧形轨道,其圆心为O′,O是轨道的最低点,M、N两点等高,O′M >>OM。连接OM的一段直线固定轨道顶端的M点有一小滑块从静止开始沿着直线轨道下滑的同时,从N点也有一小滑块从静止开始沿着圆弧轨道下滑。如果不计一切摩擦,则 ( )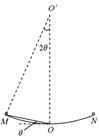
| A.两个滑块可能第一次在O点相遇 |
| B.两个滑块第一次一定在O点左方相遇 |
| C.两个滑块第一次一定在O点右方相遇 |
| D.以上三种情况均有可能 |
(3分)利用单摆测重力加速度的实验中,如果偏角足够小,但测出的重力加速度的数值偏大,可能原因是 ( )
| A.振幅较小 |
| B.测摆长时,只量出摆线的长度,没有从悬挂点量到摆球中心 |
| C.数振动次数时,少计了一次 |
| D.数振动次数时,多计了一次 |
如图所示为甲乙两单摆在同地做简谐运动的图像,则由图可知:( )
| A.甲和乙的摆长一定相同 |
| B.甲的摆球质量较小 |
| C.甲和乙的摆角一定相同 |
| D.摆到平衡位置时,甲和乙摆线所受拉力一定不相同 |
在利用单摆测定重力加速度的实验中,某同学测出了多组摆长和相应运动周期,根据实验数据,作出的T2—L关系图象如图所示,则重力加速度的计算式与由图像所得到的g值分别为(取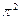 =9.87)
=9.87)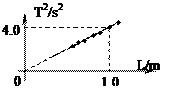
A.g=4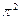 L/T2 g=9.87m/s2 L/T2 g=9.87m/s2 | B.g=4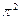 T2/L g=9.87m/s2 T2/L g=9.87m/s2 |
C.g= T2/4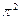 L g=9.28m/s2 L g=9.28m/s2 | D.g= L/4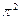 T2 g=9.28m/s2 T2 g=9.28m/s2 |
单摆摆动中,摆球经过最低点时( )
| A.摆线的张力与线长无关 |
| B.摆球的加速度与线长无关 |
| C.摆球重力的即时功率与线长无关 |
| D.摆球的动能与线长无关 |
如图4所示中给出了1、2、3、4、5共五个单摆,如果你想通过实验来验证单摆的周期与摆球的质量无关,若每次只用 两个单摆作比较,那么只需比较两次即可说明问题,
两个单摆作比较,那么只需比较两次即可说明问题, 你选用哪两组来做实验?( )
你选用哪两组来做实验?( )
| A.2和4 | B.1和3 |
| C.2和5 | D.1和4 |
一个在甲地调准的摆钟运到乙地时发现该摆钟“慢”了,其原因是( )
| A.一定是摆长变长了 |
| B.一定是摆长变了短 |
| C.可能是甲地比乙地的重力加速度大 |
D.可能是 甲地比乙地的重力加速度小 甲地比乙地的重力加速度小 |
单摆的周期在下列何种情况时会增大( )
| A.增大摆球质量 | B.减小摆长 |
| C.把单摆从赤道移到北极 | D.把单摆从海平面移到高山 |
