如图是在牛顿著作里画出的一副原理图。图中表示出从高山上用不同的水平速度抛出的物体地轨迹。物体的速度越大,落地点离山脚越远。当速度足够大时,物体将环绕地球运动,成为一颗人造地球卫星。若卫星的运动可视为匀速圆周运动,由以下哪组数据即可确定卫星的最小发射速度( )
| A.引力常数、地球质量和卫星半径; |
| B.引力常数、卫星质量和地球半径; |
| C.地球表面处重力加速度、地球半径; |
| D.地球表面处重力加速度、 地球自转周期; |
我国将要发射一颗绕月运行的探月卫星“嫦娥1号”。设该卫星的轨道是圆形的且贴近月球表面、已知月球的质量约为地球质量的  ,月球的半径约为地球半径的
,月球的半径约为地球半径的 ,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为 ( )
,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为 ( )
| A.1.8 km/s | B.0.4 km/s | C.11 km/s | D.36 km/s |
设地球半径为R,地球表面重力加速度为g,地球自转周期为T,自转角速度为ω,地球质量为M,地球的第一宇宙速度为v1,同步卫星离地球表面的高度为h,万有引力常量为G,则同步卫星的线速度大小v是
A.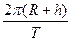 |
B.R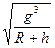 |
C.v1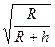 |
D.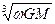 |
地球赤道上有一物体随地球的自转而做圆周运动,所受的向心力为F1,向心加速度为a1,线速度为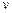 1,角速度为
1,角速度为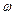 1;绕地球表面附近做圆周运动的人造卫星受的向心力为F2,向心加速度为a2,线速度为
1;绕地球表面附近做圆周运动的人造卫星受的向心力为F2,向心加速度为a2,线速度为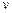 2,角速度为
2,角速度为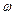 2;地球同步卫星所受的向心力为F3,向心加速度a3,线速度为
2;地球同步卫星所受的向心力为F3,向心加速度a3,线速度为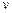 3,角度速度为
3,角度速度为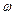 3,地球表面重力加速度为g,第一宇宙速度为
3,地球表面重力加速度为g,第一宇宙速度为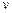 ,假设三者质量相等.则( )
,假设三者质量相等.则( )
| A.F1=F2> F3 | B.a2="g>" a3 > a1 | C.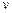 2> 2>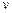 3> 3>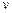 1 1 | D.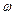 1= 1=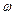 3> 3>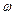 2 2 |
若某行星的质量是地球质量的6倍,半径是地球半径的1.5倍,则此行星的第一宇宙速度约为( )
| A.2 km/s | B.4 km/s |
| C.32 km/s | D.16 km/s |
我国自行研制的月球卫星“嫦娥一号”已升入太空.若已知地球质量为 ,地球半径为
,地球半径为 ,月球的质量为
,月球的质量为 ,月球的半径为
,月球的半径为 ,则“嫦娥一号”绕月球运行的速度(可认为绕月球的表面运行)是地球卫星环绕速度(即第一宇宙速度)的( )
,则“嫦娥一号”绕月球运行的速度(可认为绕月球的表面运行)是地球卫星环绕速度(即第一宇宙速度)的( )
A. 倍 倍 | B. 倍 倍 | C. 倍 倍 | D. 倍 倍 |
下列关于第一宇宙速度的说法中正确的是
| A.第一宇宙速度又称为逃逸速度 |
| B.第一宇宙速度的数值是11.2km/s |
| C.第一宇宙速度的数值是7.9km/s |
| D.第一宇宙速度是卫星绕地球运行的最小线速度 |
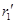 、
、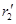 ,公转线速度分别为
,公转线速度分别为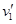 、
、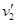 ,表面重力加速度分别为g1、g2,平均密度分别为
,表面重力加速度分别为g1、g2,平均密度分别为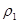 、
、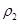 .地球第一宇宵速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是 ( )
.地球第一宇宵速度为v1,飞船贴近冥王星表面环绕线速度为v2,则下列关系正确的是 ( )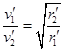
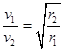
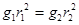
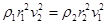
 ,已知该星球半径为R,万有引力常量为G,求:
,已知该星球半径为R,万有引力常量为G,求:
