2007年10月25日17时55分,北京航天飞行控制中心对“嫦娥一号”卫星实施首次变轨控制并获得成功。这次变轨是在卫星运行到远地点时实施的,而此后将要进行的3次变轨均在近地点实施。“嫦娥一号”卫星的首次变轨之所以选择在远地点实施,是为了抬高卫星近地点的轨道高度。同样的道理,要抬高远地点的高度就需要在近地点变轨。如图为“嫦娥一号”卫星某次在近地点A由轨道1变轨为轨道2的示意图,下列说法中正确的是( )
| A.“嫦娥一号”在轨道1的A点处应点火加速 |
| B.“嫦娥一号”在轨道1的A点处的速度比在轨道2的A点处的速度大 |
| C.“嫦娥一号”在轨道1的B点处的加速度比在轨道2的C点处的加速度大 |
| D.“嫦娥一号”在轨道1的B点处的机械能比在轨道2的C点处的机械能大 |
我国已成功发射多颗气象卫星,为气象预报提供了大量有效信息,其中“风云一号”是极地圆形轨道卫星,“风云二号”是地球同步卫星。且“风云一号”的运行周期是“风云二号”的一半,比较这两颗卫星,下列说法中正确的是
| A.“风云一号”离地面较近,对同一区域连续观测时间长 |
| B.“风云二号”离地面较近,观测覆盖区域大 |
| C.“风云一号”运行线速度较大,观测覆盖区域大 |
| D.“风云二号”运行线速度较大,对同一区域连续观测时间长 |
如图所示,a、b、c是在地球大气层外圆形轨道上运行的3颗人造卫星,下列说法正确的是
| A.b、c的线速度大小相等,且大于a的线速度 |
| B.b、c的向心加速度大小相等,且大于a的向心加速度 |
| C.c加速可追上同一轨道上的b,b减速可等候同一轨道上的c |
| D.a卫星由于某种原因,轨道半径缓慢减小,其线速度将变大 |
人造卫星绕地球做匀速圆周运动,它所受的向心力F跟轨道半径r的关系是
A.由公式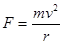 可知F和r成反比 可知F和r成反比 | B.由公式F=mω2r可知F和r成正比 |
| C.由公式F=mωv 可知F和r无关 | D.由公式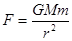 可知F和r2成反比 可知F和r2成反比 |
如图所示,“神舟”飞船升空后,进入近地点为B,远地点为A的椭圆轨道Ⅰ上飞行。飞行数圈后变轨。在过远地点A的圆轨道Ⅱ上做匀速圆周运动.飞船由椭圆轨道Ⅰ运行变轨到圆形轨道Ⅱ运行后( )
| A.周期变短.机械能增加 |
| B.周期变短,机械能减小 |
| C.周期变长,机械能增加 |
| D.周期变长,机械能减小 |
“天宫一号”被长征二号火箭发射后,准确进入预定轨道,如图所示,“天宫一号”在轨道1上运行4周后,在Q点开启发动机短时间加速,关闭发动机后,“天宫一号”沿椭圆轨道2运行到达P点,开启发动机再次加速,进入轨道3绕地球作圆周运动,“天宫一号”在图所示轨道1、2、3上正常运行时,下列说法正确的是( ) 
| A.“天宫一号”在轨道3上的速率大于在轨道1上的速率。 |
| B.“天宫一号”在轨道3上的角速度小于在轨道1的角速度 |
| C.“天宫一号”在轨道1上经过Q点的加速度大于它在轨道2上经过Q点的加速度 |
| D.“天宫一号”在轨道2上经过P点的加速度等于它在轨道3上经过P点的加速度 |
随着航空航天技术的迅猛发展,深太空探测已逐渐成为科学界关注的热点。假设在深太空探测中发现有一颗星球“G”,其质量是地球质量的2倍,其半径是地球半径的一半。则下列判断正确的是 ( )
| A.在星球“G”上发射同步卫星,其周期一定小于地球同步卫星的周期 |
| B.某物体在星球“G”表面所受重力是它在地球表面所受重力的8倍 |
| C.在星球“G”上的第一宇宙速度是在地球上第一宇宙速度的2倍 |
| D.绕星球“G”运行的人造卫星和以相同轨道半径绕地球运行的人造卫星线速度相同 |
甲、乙为两颗地球卫星,其中甲为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨道均可视为圆轨道。以下判断正确的是
| A.甲的周期大于乙的周期 | B.乙的速度大于第一宇宙速度 |
| C.甲的加速度小于乙的加速度 | D.甲在运行时能经过北极的正上方 |
由地面发射一颗人造卫星绕地球作匀速圆周运动,轨道半径为r,卫星动能为Ek。如果发射的这颗卫星匀速园周运动的半径是2r,则下列说法中正确的是
| A.发射卫星所消耗的能量增大 | B.卫星在轨道上的动能增大为2Ek |
C.卫星在轨道上的动能减小为 | D.卫星在轨道上的机械能增大 |
神舟八号飞船绕地球做匀速圆周运动时,飞行轨道在地球表面的投影如图所示,图中标明了飞船相继飞临赤道上空所对应的地面的经度。设神舟八号飞船绕地球飞行的轨道半径为r1,地球同步卫星飞行轨道半径为r2.则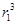 ∶
∶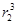 等于
等于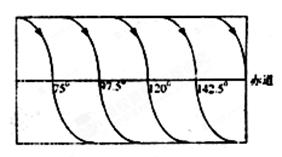
| A.1∶24 | B.1∶156 |
| C.1∶256 | D.1∶210 |