设地球的质量为M,半径为R,自转的角速度为ω,地球表面的重力加速度为g,万有引力恒量为G,同步卫星轨道半径为r,则同步卫星的速度为: ( )
A.v= . . | B.v=ωr | C.v= | D.v= |
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3。轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中 正确的是( )
正确的是( )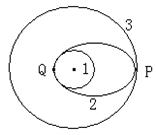
| A.卫星在轨道3上的速率大于在轨道1上的速率 |
B.卫星在轨道3上的角 速度大于在轨道1上的角速度 速度大于在轨道1上的角速度 |
| C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 |
| D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 |
两颗人造地球卫星A和B,分别在不同轨道上绕地球做匀速圆周运动,两卫星的轨道半径分别为rA和rB,且rA> rB,则A和B两卫星比较,下列说法正确的是
| A.卫星A受到地球引力较小 | B.卫星A的运行速率较小 |
| C.卫星B的运动周期较大 | D.卫星A的机械能较大 |
某人造卫星绕地球做匀速圆周运动,设地球半径为R,地面重力加速度为g,下列说法正确的是
A.人造卫星的最小周期为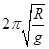 |
B.卫星在距地面高度为R处的绕行速度为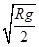 |
C.卫星在距地面高度为R处的重力加速度为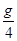 |
| D.地球同步卫星的速率比近地卫星速率小,所以发射同步卫星所需的能量较少 |
三颗人造卫星a、b、c绕地球作圆周运动,a与b的质量相等并小于c的质量,b和c的轨道半径相等且大于a的轨道半径,则
| A.卫星b、c运行的速度大小相等,且大于a的速度大小 |
| B.卫星b、c周期相等,且大于a的周期 |
| C.卫星b、c向心加速度大小相等,且大于a的向心加速度 |
| D.卫星b所需的向心力最小 |
2008年9月我国成功发射了“神州七号”载人飞船。为了观察“神舟七号“的运行和宇航员仓外活动情况,飞船利用弹射装置发射一颗“伴星“。伴星经调整后,和”神舟七号“一样绕地球做匀速圆周运动,但比“神舟七号“离地面稍高一些,如图所示,那么:
| A.伴星的运行周期比“神舟七号“稍大一些 |
| B.伴星的运行速度比“神舟七号“稍大一些 |
| C.伴星的运行角速度比“神舟七号“稍大一些 |
| D.伴星的向心加速度比“神舟七号“稍大一些 |
已知万有引力常量G,地球的半径R,地球表面重力加速度g,地球自转周期T,不考虑地球自转对重力的影响。利用以上条件不可能求的物理量有
| A.地球的质量和密度 |
| B.地球同步卫星的轨道高度 |
| C.第一宇宙速度 |
| D.第三宇宙速度 |
某探月卫星经过多次变轨,最后成为一颗月球卫星。设该卫星的轨道为圆形,且贴近月球表面,则该近月卫星的运行速率约为(已知月球的质量约为地球质量的1/81,月球
半径约为地球半径的1/4,近地地球卫星的速率为7.9 km/s)( )
| A.1.8 km/s | B.0.4 km/s | C.11 km/s | D.36 km/s |
因“光纤之父”高锟的杰出贡献,早在1996年中国科学院紫金山天文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。假设高锟星为均匀的球体,其质量为地球质量的1/k倍,半径为地球半径的1/q倍,则“高锟星”表面的重力加速度是地球表面的重力加速度的 [ ]
| A.q/k倍 | B.k/q倍 | C.q2/k倍 | D.k2/q倍 |
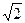 倍
倍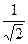 倍
倍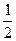 倍
倍