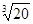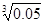天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和运动周期.由此可推算出 ( )
| A.行星的质量 | B.行星的半径 |
| C.恒星的质量 | D.恒星的半径 |
我国将独立建立自己的空间站,未来宇航员乘返回舱返回地球时,返回舱高速进入大气层后,受到空气阻力的作用而减速,接近地面时,减速伞打开,在距地面几米处,制动发动机点火制动,返回舱迅速减速,安全着陆,下列说法正确的是( )
| A.返回舱脱离空间站后需要减速,然后进入一个返程的椭圆轨道 |
| B.返回舱进入大气层运动过程,所阻力所做功等于其动能的变化 |
| C.引力始终对返回舱做正功,所以返回舱的机械能增加 |
| D.制动发动机点火制动时,返回舱处于超重状态 |
如右图,三个质点a、b、c质量分别为m1、m2、M(M>> m1,M>> m2)。在c的万有引力作用下,a、b在同一平面内绕c沿逆时针方向做匀速圆周运动,它们的周期之比Ta∶Tb=1∶k;从图示位置开始,在b运动一周的过程中,则 ( )
| A.a、b距离最近的次数为k次 |
| B.a、b距离最近的次数为k+1次 |
| C.a、b、c共线的次数为2k |
| D.a、b、c共线的次数为2k-2 |
“嫦娥一号”探月卫星沿地月转移轨道到达月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如右图所示。之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动。用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期,用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度,v1、v2、v3分别表示卫星沿三个轨道运动到P点的速度,用F1、F2、F3分别表示卫星沿三个轨道运动到P点时受到的万有引力,则下面关系式中正确的是( )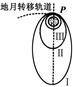
| A.a1<a2<a3 |
| B.v1<v2<v3 |
| C.T1>T2>T3 |
| D.F1=F2=F3 |
如图所示,A和B两行星绕同一恒星C做圆周运动,旋转方向相同,A行星的周期为T1,B行星的周期为T2,某一时刻两行星相距最近,则 ( )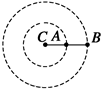
| A.经过T1+T2两行星再次相距最近 |
| B.经过两行星再次相距最近 |
| C.经过两行星相距最远 |
| D.经过两行星相距最远 |
已知某行星绕太阳做匀速圆周运动的半径为r,公转周期为T,万有引力常量为G,下列说法正确的是
| A.可求出行星的质量 |
| B.可求出太阳的质量 |
| C.可求出行星的绕行速度 |
D.据公式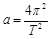 ,行星的向心加速度与半径r成正比 ,行星的向心加速度与半径r成正比 |
探测器探测到土星外层上有一个小环,为了判断它是土星的一部分还是土星的卫星群,可以测量环中各层的线速度v与该层到土星中心的距离R之间的关系来确定
| A.若v∝R,则该环是土星的一部分 | B.若v2∝R,则该环是土星的卫星群 |
| C.若 v∝1/R,则该环是土星的一部分 | D.若v2∝1/R,则该环是土星的卫星群 |
火星有两颗卫星,分别是火卫一和火卫二,它们的轨道近似为圆。已知火卫一的周期为7小时39分。火卫二的周期为30小时18分,则两颗卫星相比
| A.火卫一距火星表面较近。 | B.火卫二的质量较大 |
| C.火卫二运动速度较大。 | D.火卫二的向心加速度较大 |