火星有两颗卫星,分别是火卫一和火卫二,它们的轨道近似为圆。已知火卫一的周期为7小时39分。火卫二的周期为30小时18分,则两颗卫星相比( )
| A.火卫一距火星表面较近 | B.火卫二的角速度较大 |
| C.火卫一的运动速度较大 | D.火卫二的向心加速度较大 |
当一个做匀速圆周运动的人造卫星的轨道半径增大到原来的2倍时,则( )
| A.卫星的线速度也增大到原来的2倍 | B.卫星所需向心力减小到原来的1/2倍 |
C.卫星的线速度减小到原来的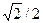 倍 倍 | D.卫星所需向心力减小到原来的1/4倍 |
最近,科学家在望远镜中看到太阳系外某恒星有一行星,并测得它围绕恒星运动一周所用的时间为1200 年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个救据可以求出的量有( )
| A.恒星质量与太阳质量之比 | B.恒星密度与太阳密度之比 |
| C.行星质量与地球质量之比 | D.行星运行速度与地球公转速度之比 |
我国发射的神舟五号宇宙飞船的周期约为90min,如果把它绕地球的运动看作是匀速圆周运动,飞船的运动和一颗周期为120 min的绕地球作匀速圆周运动的人造地球卫星相比,下列判断中正确的是( )
| A.飞船的轨道半径大于卫星的轨道半径 |
| B.飞船的运行速度小于卫星的运行速度 |
| C.飞船运动的角速度小于卫星运动的角速度 |
| D.飞船运动的向心加速度大于卫星运动的向心加速度 |
假如一人造地球卫星做匀速圆周运动的轨道半径增大到原来的2倍,仍做匀速圆周运动。则


| A.根据公式V=rω可知卫星的线速度将增大到原来的2倍 |
| B.根据公式F=mv2/r,可知卫星所受的向心力将变为原来的1/2 |
| C.根据公式F=GMm/r2,可知地球提供的向心力将减少到原来的1/4 |
| D.根据上述B和C给出的公式,可知卫星运动的线速度将减少到原来的/2 |
卡文迪许实验室是科学家的摇篮,孕育了将近30名诺贝尔物理学奖获得者,卡文迪许在实验室测出了万有引力常量G,卡文迪许把自己的实验说成是“称量地球的质量”,根据万有引力常量G,再结合下面的数据能够测量地球质量或密度的是:( )
| A.人造地球卫星的运行周期和运行半径,可以计算地球的质量 |
| B.人造地球卫星的运行周期和运行半径,可以计算地球的密度 |
| C.近地人造地球卫星的运行周期,可以计算地球的质量 |
| D.近地人造地球卫星的运行周期,可以计算地球的密度 |
三颗人造卫星 、
、 、
、 在地球的大气层外沿如图所示的方向做匀速圆周运动,
在地球的大气层外沿如图所示的方向做匀速圆周运动, ,则三颗卫星
,则三颗卫星
A.线速度大小: | B.周期: |
C.向心力大小: | D.轨道半径和周期的关系: |
银河系的恒星中大约四分之一是双星,两星在相互之间的万有引力作用下绕两者连线上某一定点C做同周期的匀速圆周运动。由天文观察测得其运动周期为T,两星与轴的距离分别为R1和R2,已知万有引力常量为G,那么下列说法中正确的是:
| A.这两颗星的质量一定相等 | B.这两颗星的角速度大小一定相等 |
C.这两颗星的质量之比为  | D.这两颗星的线速度之比为 |
我国发射的“神州六号”载人飞船,与“神州五号”飞船相比,它在更高的轨道上绕地球做匀速圆周运动,如图做示,下列说法中正确的是: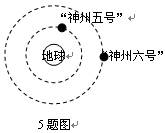
| A.“神州六号”运行速度较大 |
| B.“神州六号”运行角速度较大 |
| C.“神州六号”运行周期较大 |
| D.“神州六号”运行的向心加速度较小 |



