下表是火星和地球部分数据对照表,把火星和地球视为质量均匀的理想球体,它们绕太阳的运动近似看作匀速圆周运动,从表中数据可以分析得出
| | 质量(千克) | 公转周期(天) | 自转周期 (小时) | 近似公转轨道半径(米) | 星球半径(米) |
| 火星 | 6.421×1023 | 686.98 | 24.62 | 2.28×1011 | 3.395×106 |
| 地球 | 5.976×1024 | 365.26 | 23.93 | 1.50×1011 | 6.378×106 |
B.地球公转的动能较小
C.火星两极处地表重力加速度较大
D.火星的第一宇宙速度较大
(基础卷)假设人造卫星绕地球做匀速圆周运动,当卫星绕地球运动的轨道半径增大到原来的2倍时,则有( )
| A.卫星运动的线速度将增大到原来的2倍 |
| B.卫星所受的向心力将减小到原来的一半 |
| C.卫星运动的周期将增大到原来的2倍 |
D.卫星运动的线速度将减小到原来的 |
(专题卷)2007年10月24日,我国发射了第一颗探月卫星——“嫦娥一号” ,使“嫦娥奔月”这一古老的神话变成了现实.嫦娥一号发射后先绕地球做圆周运动,经多次变轨,最终进入距月面h=200公里的圆形工作轨道,开始进行科学探测活动.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列说法正确的( )
A.嫦娥一号绕月球运行的周期为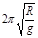 |
B.由题目条件可知月球的平均密度为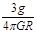 |
C.嫦娥一号在工作轨道上的绕行速度为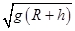 |
D.在嫦娥一号的工作轨道处的重力加速度为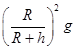 |
(专题卷)发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。则在卫星分别在1、2、3轨道上正常运行时,以下说法正确的是:( )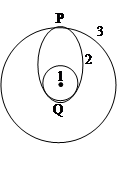
| A.卫星在轨道3上的速率大于在轨道1上的速率。 |
| B.卫星在轨道3上的角速度小于在轨道1上的角速度。 |
| C.卫星在轨道1上运动一周的时间小于于它在轨道2上运动一周的时间。 |
| D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度。 |
中国志愿者王跃参与人类历史上第一次全过程模拟从地球往返火星的一次试验“火星-500”,王跃走出登陆舱,成功踏上模拟火星表面,在“火星”上首次留下中国人的足迹,目前正处于从“火星”返回地球途中.假设将来人类一艘飞船从火星返回地球时,经历如图所示的变轨过程,则下列说法正确的是 ( )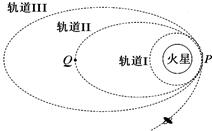
| A.飞船在轨道Ⅱ上运动时,在P点的速度大于在Q点的速度 |
| B.飞船在轨道Ⅰ上运动的机械能大于在轨道Ⅱ上运动的机械能 |
| C.飞船在轨道Ⅰ上运动到P点时的加速度等于飞船在轨道Ⅱ上运动到P点时的加速度 |
| D.飞船绕火星在轨道Ⅰ上运动的周期跟飞船返回地面的过程中绕地球以轨道I同样的半径运动的周期相同 |
“科学真是迷人。”如果我们能测出月球表面的加速度g、月球的半径R和月球绕地球运转的周期T,就能根据万有引力定律“称量”月球的质量了。已知引力常数G,用M表示月球的质量。关于月球质量,下列说法正确的是( )
A.M =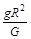 | B.M =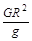 |
C.M =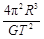 | D.M =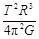 |
地球赤道上有一物体随地球的自转而做圆周运动,所需的向心力为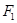 ,向心加速度为
,向心加速度为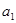 ,线速度为
,线速度为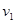 ,角速度为
,角速度为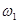 ;绕地球表面附近做圆周运动的人造卫星(高度忽略)所需的向心力为
;绕地球表面附近做圆周运动的人造卫星(高度忽略)所需的向心力为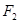 ,向心加速度为
,向心加速度为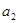 ,线速度为
,线速度为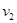 ,角速度为
,角速度为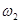 ;地球同步卫星所需的向心力为
;地球同步卫星所需的向心力为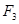 ,向心加速度为
,向心加速度为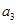 ,线速度为
,线速度为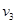 ,角速度为
,角速度为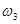 。设三者质量相等,则( )
。设三者质量相等,则( )
A.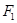 = =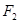 > >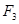 | B.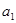 = =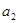 > >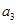 |
C.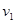 = =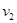 > >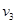 | D.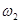 > >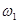 = =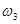 |
两个行星各有一个卫星绕其表面运行,已知两个卫星的周期之比为1∶2,两行星半径之比为2∶1,有下列结论①两行星密度之比为4∶1 ②两行星质量之比为16∶1 ③两行星表面处重力加速度之比为8∶1 ④两卫星的速率之比为4∶1,正确的有
| A.①② | B.①②③ | C.②③④ | D.①③④ |
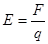 .在引力场中可以有一个类似的物理量用来反映各点引力场的强弱.设地球质量为M,半径为R,地球表面处重力加速度为g,引力常量为G.如果一个质量为m的物体位于距地心2R处的某点,则下列表达式中能反映该点引力场强弱的是( )
.在引力场中可以有一个类似的物理量用来反映各点引力场的强弱.设地球质量为M,半径为R,地球表面处重力加速度为g,引力常量为G.如果一个质量为m的物体位于距地心2R处的某点,则下列表达式中能反映该点引力场强弱的是( )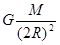
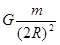
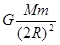
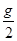
 约45km,质量
约45km,质量 和半径
和半径 (其中
(其中 为光速
为光速 为引力常量),则该黑洞表面重力加速度的数量级
为引力常量),则该黑洞表面重力加速度的数量级 


