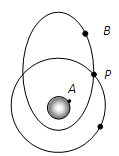
一宇宙飞船绕地心做半径为r的匀速圆周运动,飞船舱内有一质量为m的人站在可称体重的台秤上.用R表示地球的半径,g表示地球表面处的重力加速度,g′表示宇宙飞船所在处的地球引力加速度,FN表示人对秤的压力,下面说法中正确的是 ( )
| A.g′=0 | B.g′=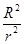 g g |
| C.FN=0 | D.FN=m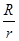 g g |
有一宇宙飞船到了某行星上(该行星没有自转运动),以速度v接近行星赤道表面匀速飞行,测出运动的周期为T,已知引力常量为G,则可得 ( )
A.该行星的半径为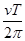 |
B.该行星的平均密度为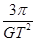 |
| C.无法测出该行星的质量 |
D.该行星表面的重力加速度为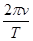 |
牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律.在创建万有引力定律的过程中,牛顿 ( )
| A.接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 |
| B.根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即F∝m的结论 |
| C.根据F∝m和牛顿第三定律,分析了地月间的引力关系,进而得出F∝m1m2 |
| D.根据大量实验数据得出了比例系数G的大小 |
某星球的质量约为地球质量的9倍,半径约为地球半径的一半,若从地球表面高h处平抛一物体,射程为60 m,则在该星球上,从同样高度以同样的初速度平抛同一物体,射程应为 ( )
| A.10 m | B.15 m | C.90 m | D.360 m |
天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和运动周期.由此可推算出 ( )
| A.行星的质量 | B.行星的半径 |
| C.恒星的质量 | D.恒星的半径 |
“嫦娥一号”月球探测器在环绕月球运行过程中,设探测器运行的轨道半径为r,运行速率为v,当探测器在飞越月球上一些环形山中的质量密集区上空( )
| A.r、v 都将略为减小 |
| B.r、v都将保持不变 |
| C.r将略为减小,v将略为增大 |
| D.r将略为增大,v将略为减小 |
火星的质量和半径分别约为地球的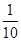 和
和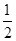 ,地球表面的重力加速度为g,则火星表面的重力加速度约为 ( )
,地球表面的重力加速度为g,则火星表面的重力加速度约为 ( )
| A.0.2g | B.0.4g | C.2.5g | D.5g |
宇宙中两个星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法错误的是 ( )
| A.双星相互间的万有引力减小 |
| B.双星圆周运动的角速度增大 |
| C.双星圆周运动的周期增大 |
| D.双星圆周运动的半径增大 |
宇宙飞船在半径为R1的轨道上运行,变轨后的半径为R2,R1>R2,宇宙飞船绕地球做匀速圆周运动,则变轨后宇宙飞船的 ( )
| A.线速度变小 | B.角速度变小 |
| C.周期变大 | D.向心加速度变大 |