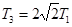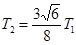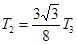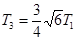下列几组数据中能算出地球质量的是（万有引力常量G是已知的）

2012年2月25日0时12分,西昌卫星发射中心用“长征三号丙”运载火箭，成功将第11颗北斗导航卫星送入了太空预定轨道. 这是一颗地球同步卫星, 若卫星离地心距离为r，运行速率为v₁，加速度为a₁，地球赤道上的物体随地球自转的向心加速度为a₂，第一宇宙速度为v₂,，地球半径为R，则 (    )

A．＝

B．=

C．=

D．＝

极地卫星的运行轨道平面通过地球的南北两极（轨道可视为圆轨道）。如图所示，若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方，所用时间为t，已知地球半径为R（地球可看做球体），地球表面的重力加速度为g，引力常量为G，由以上条件可知 

A．地球的质量为	B．卫星运行的角速度为
C．卫星运行的线速度为	D．卫星距地面的高度

我国发射了探月卫星“嫦娥2号”。假设该卫星的绕月轨道是圆形的，且贴近月球表面。已知月球的质量约为地球质量的l/81，月球的半径约为地球半径的l/4，地球上的第一宇宙速度约为7.9km/s，则该探月卫星绕月运行的速率约为

关于开普勒第三定律中的公式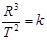，下列说法中正确的是（ ）

我们研究了开普勒第三定律，知道了环绕天体绕中心天体的运动轨道近似是圆形，轨道半径 R的三次方与周期T的平方的比为常数，则该常数的大小 (  )

1789年英国著名物理学家卡文迪许首先估算出了地球的平均密度．根据你所学过的知识，估算出地球密度的大小最接近 （   ）（地球半径R=6400km，万有引力常量G=6.67×10^-11N·m²/kg²）

由于通讯和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的（      ）

2011年9月29日，“天宫一号”顺利升空，11月1日，“神舟八号”随后飞上太空，11月3日凌晨“神八”与离地高度343km轨道上的“天宫一号”对接形成组合体，中国载人航天首次空间交会对接试验获得成功，为建立太空实验室——空间站迈出了关键一步。设对接后的组合体在轨道上做匀速圆周运动，则下列说法中正确的是                                   （   ）  
                                         

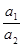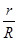
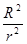
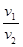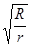
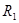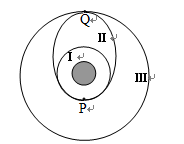
如图所示，某次发射远地圆轨道卫星时，先让卫星进入一个近地的圆轨道Ⅰ，在此轨道运行的卫星的轨道半径为、周期为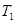；然后在P点点火加速，进入椭圆形转移轨道Ⅱ，在此轨道运行的卫星的周期为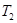；到达远地点Q时再次点火加速，进入远地圆轨道Ⅲ，在此轨道运行的卫星的轨道半径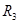为、周期为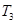（轨道Ⅱ的近地点为Ⅰ上的P点，远地点为轨道Ⅲ上的Q点）。已知＝2，则下列关系正确的是

A．	B．
C．	D．