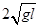如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为l?质量为m?粗细均匀?质量分布均匀的软绳置于斜面上,其上端与斜面顶端齐平.用细线将物块与软绳连接,物块由静止释放后向下运动,直到软绳刚好全部离开斜面(此时物块未到达地面),在此过程中( )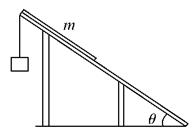
| A.物块的机械能逐渐增加 |
B.软绳重力势能共减少了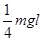 |
| C.物块重力势能的减少等于软绳克服摩擦力所做的功 |
| D.软绳重力势能的减少小于其动能的增加与克服摩擦力所做功之和 |
如图所示,物体沿30°的固定斜面以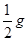 (g为本地的重力加速度大小)的加速度匀减速上升,则在此过程中,物体的机械能是( )
(g为本地的重力加速度大小)的加速度匀减速上升,则在此过程中,物体的机械能是( )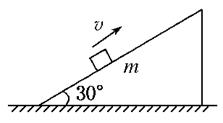
| A.不变的 | B.减小的 |
| C.增加的 | D.不能判断 |
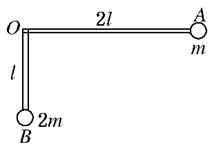
如图所示,A?B质量均为m,轻质小滑轮距光滑水平杆高度为H,开始时轻质细绳与杆夹角α=45°.释放B后,A?B同时开始运动,小滑轮绕轴无摩擦转动.则在A?B开始运动以后,下列说法正确的是( )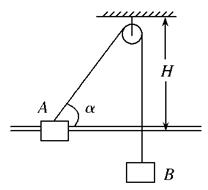
| A.A?B速度同时达到最大值 |
| B.轻质细绳一直对B做负功 |
C.A能获得的最大动能为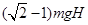 |
| D.B将在竖直方向做简谐运动 |
一根长为l的不可伸长的轻绳,一端系一小球,另一端悬挂于O点.将小球拉起使轻绳拉直并与竖直方向在60°角,如图所示,在O点正下方有A?B?C三点,并且有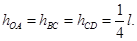 当在A处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hA;当在B处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hB;当在C处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度hC,则小球摆动的最大高度hA?hB?hC之间的关系是( )
当在A处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hA;当在B处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度为hB;当在C处钉钉子时,小球由静止下摆,被钉子挡住后继续摆动的最大高度hC,则小球摆动的最大高度hA?hB?hC之间的关系是( )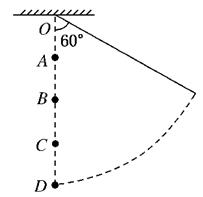
| A.hA=hB=hC | B.hA>hB>hC |
| C.hA>hB=hC | D.hA=hB>hC |
如图,一很长的?不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧,从静止开始释放b后,a可能达到的最大高度为( )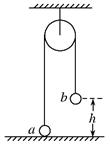
| A.h | B.1.5h |
| C.2h | D.2.5h |
伽利略的斜面实验反映了一个重要事实:如果空气阻力和摩擦力小到可以忽略不计,小球一但沿斜面A滚落,必将准确地终止于斜面B上同它开始点相同高度处,绝不会更高一点,这说明,小球在运动过程中有一个“东西”是不变的,这个“东西”是
| A.弹力 | B.速度 |
| C.动量 | D.能量 |
如图所示,质量为m的钩码在一个弹簧秤的作用下竖直向上运动。设弹簧秤的示数为T,不计空气阻力,重力加速度为g。则下列说法中正确的是
| A.T=mg时,钩码的机械能不变 |
| B.T<mg时,钩码的机械能减小 |
| C.T<mg时,钩码的机械能增加 |
| D.T>mg时,钩码的机械能不变 |