如右图所示,一个半径为R的圆轨道竖直固定在水平地面上,斜面AB与圆轨道在B点相切,在圆轨道B点处开有一小孔,有一可看作质点的小球从斜面上距离地面高为h的A点无初速滚下,从B点进入圆轨道,所有摩擦不计。关于小球的运动情况,下述说法中正确的是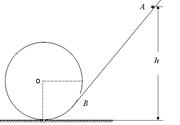
A.只有当h≥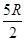 ,小球才不会脱离轨道 ,小球才不会脱离轨道 |
| B.只要当h≥2R,小球就不会脱离轨道 |
| C.当h≥R时,小球一定会脱离圆轨道 |
| D.当h<R 时,小球不会脱离轨道 |
面积很大的水池,水深为H,水面上浮着一正方体木块,木块边长为a,密度为水的1/2,质量为m.开始时,木块静止,有一半没入水中,如图所示.现用力将木块缓慢地压到池底.在这一过程中( )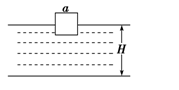
A.木块的机械能减少了mg(H-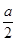 ) ) |
| B.水池中水的机械能不变 |
C.水池中水的机械能增加了2mg(H-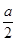 ) ) |
D.水池中水的机械能增加了2mg(H-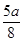 ) ) |
如图所示,离水平地面一定高处水平固定一内壁光滑的圆筒,筒内固定一轻质弹簧,弹簧处于自然长度.现将一小球从地面以某一初速度斜向上抛出,刚好能水平进入圆筒中,不计空气阻力.下列说法中正确的是( )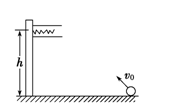
| A.弹簧获得的最大弹性势能小于小球抛出时的动能 |
| B.小球从抛出到将弹簧压缩到最短的过程中小球的机械能守恒 |
| C.小球抛出的初速度大小仅与圆筒离地面的高度有关 |
| D.小球从抛出点运动到圆筒口的时间与小球抛出时的角度无关 |
(2011年杭州第一次模拟)如图所示,小车上有固定支架,一可视为质点的小球用轻质细绳拴挂在支架上的O点处,且可绕O点在竖直平面内做圆周运动,绳长为L.现使小车与小球一起以速度v0沿水平方向向左匀速运动,当小车突然碰到矮墙后,车立即停止运动,此后小球上升的最大高度不可能是( )
A.大于 | B.小于 |
C.等于 | D.等于2L |
如图所示,在两个质量分别为m和2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),而小球可绕穿过轻杆中心O的水平轴无摩擦转动,现让轻杆处于水平位置,然后无初速度释放,重球b向下,轻球a向上,产生转动,在杆转至竖直的过程中( )
| A.b球的重力势能减小,动能增加 |
| B.a球的重力势能增加,动能减小 |
| C.a球和b球的总机械能守恒 |
| D.a球和b球的总机械能不守恒 |
(2011年河南安阳质检)ABCD是一段竖直平面内的光滑轨道,AB段与水平面成α角,CD段与水平面成β角,其中BC段水平,且其长度大于L.现有两小球P、Q,质量分别是2m、m,用一长为L的轻质直杆连接,将P、Q由静止从高H处释放,在轨道转折处用光滑小圆弧连接,不考虑两小球在轨道转折处的能量损失.则小球P滑上CD轨道的最大高度h为( )
| A.h=H |
B.h=H+ |
| C.h=H+Lsinβ |
D.h=H+ |
(2011年东北地区名校联考)如图所示,一物体以速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法正确的是( )
| A.若把斜面从C点锯断,由机械能守恒定律知,物体冲出C点后仍能升高h |
| B.若把斜面弯成如图所示的半圆弧形,物体仍能沿AB′升高h |
| C.若把斜面从C点锯断或弯成如图所示的半圆弧形,物体都不能升高h,因为物体的机械能不守恒 |
| D.若把斜面从C点锯断或弯成如图所示的半圆弧形,物体都不能升高h,但物体的机械能仍守恒 |



