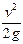一根轻弹簧的一端拴一个物体A,把物体A提到与悬点O在同一水平面的位置(弹簧处于原长),如图所示,然后由静止释放,在A摆向最低点的过程中,若不计空气阻力,则( )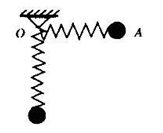
| A.物体A的机械能能守恒 |
| B.物体A的械能能减少 |
| C.物体A的机械能增大 |
| D.弹簧的弹力对物体A不做功 |
如图,一轻弹簧左端固定在长木块M的左端,右端与小木块m连接,且m、M及M与地面间接触光滑。开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2。在两物体开始运动以后的整个运动过程中,对m、M和弹簧组成的系统(整个过程中弹簧形变不超过其弹性限度),正确的说法是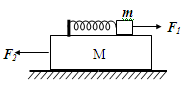
| A.由于F1、F2等大反向,故系统动量守恒,机械能也守恒 |
| B.F1、F2分别对m、M做正功,故系统机械能不断增加 |
| C.当弹簧弹力大小与F1、F2大小相等时,系统机械能最大 |
| D.系统机械能最大时,两物体动能都为零 |
如图所示,将倾角为30°的斜面体置于水平地面上,一根不可伸长的轻绳两端分别系着小球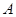 和物块
和物块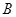 ,跨过固定于斜面体顶端的光滑支点
,跨过固定于斜面体顶端的光滑支点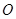 。已知
。已知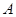 的质量为
的质量为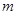 ,
,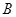 的质量为
的质量为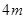 。现用手托住
。现用手托住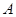 ,使
,使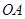 段绳恰处于水平伸直状态(绳中无拉力),
段绳恰处于水平伸直状态(绳中无拉力),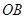 绳平行于斜面,此时物块
绳平行于斜面,此时物块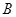 恰好静止不动。将
恰好静止不动。将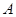 由静止释放,在其下摆过程中,斜面体与物块
由静止释放,在其下摆过程中,斜面体与物块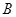 始终保持静止,下列判断中正确的是
始终保持静止,下列判断中正确的是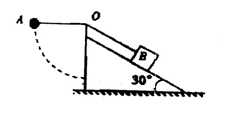
A.物块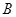 受到的摩擦力先减小后增大 受到的摩擦力先减小后增大 |
B.物块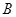 受到的摩擦力不变 受到的摩擦力不变 |
C.小球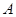 与地球组成的系统机械能守恒 与地球组成的系统机械能守恒 |
D.小球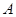 与地球组成的系统机械能不守恒 与地球组成的系统机械能不守恒 |
将一个动力传感器连接到计算机上,我们就可以测出快速变化的力,图所示为用这样方法测得的某小滑块在半球形碗内在竖直平面内来回自由滑动时,对碗的压力随时间的变化曲线(某一段时间内),根据曲线得的信息分析小滑块在该段时间内的运动,下列判断正确的是:(g=10m/s2)
| A.小滑块能滑到的最高点与圆心等高 |
| B.小滑块在滑动时所受的摩擦力为零 |
| C.小滑块在滑动的过程中机械能守恒 |
| D.小滑块的质量为0.3kg |
当物体受到的合外力的功为零时
| A.物体受到的合外力一定为零 | B.物体的动能一定不变 |
| C.物体的动量一定不变 | D.物体的机械能一定不变 |
如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量为M和m的小球,两杆之间的距离为d,两球用自由长度为d的轻质弹簧连接,现从左侧用挡板将M球挡住,再用力把m球向左拉一段距离(在弹性限度以内)后自静止释放,释放后,下面判断中正确的是 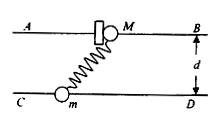
| A.在弹簧第一次恢复原长的过程中,两球和弹簧组成的系统动量守恒、机械能守恒 |
| B.弹簧第二次恢复原长时,M和m球的速度相等 |
| C.弹簧第一次恢复原长后,继续运动的过程中,系统的动量不守恒、机械能守恒 |
| D.释放m以后的运动过程中,弹簧的最大伸长量总小于运动开始时的弹簧伸长量 |
如图所示,M为固定在水平桌面上的有缺口的方形木块,abcd为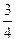 圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度。今将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处切入轨道内运动,不计空气阻力,则( )
圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度。今将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处切入轨道内运动,不计空气阻力,则( )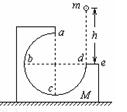
| A.在h一定的条件下,释放后小球的运动情况与小球的质量有关 |
| B.只要改变h的大小,就能使小球通过a点后,既可能落回轨道内,又可能落到de面上 |
| C.无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内 |
| D.调节h的大小,使小球飞出de面之外(即e的右面)是可能的 |
一物体从某一高度自由落下,落在直立于地面的轻弹簧上,如图所示,在A点,物体开始与弹簧接触,到B点时,物体速度为零,然后被弹回。下列说法中正确的是
| A.物体从A下降到B的过程中,速率不断变小 |
| B.物体在B处时,其加速度大于重力加速度 |
| C.物体从B下降到A的过程中,物体的机械能守恒 |
| D.物体从A下降到B的过程中,物体的加速度不断增大 |
在空军演习中,某空降兵从飞机上跳下,他从跳离飞机到落地的过程中沿竖直方向运动的v-t图像如图所示,则下列说法正确的是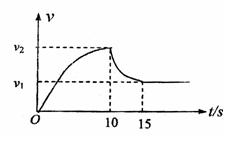 ?
?
| A.0~10s内空降兵和伞整体所受重力大于空气阻力 |
| B.第10s末空降兵打开降落伞,此启做匀减速运动至第15s末? |
| C.10s~15s空降兵竖直方向的加速度向上,加速度大小在逐渐减小。? |
| D.15s后空降兵保持匀速下落,此过程中机械能守恒。 |