一座大楼中有一部直通高层的客运电梯,电梯的简化模型如图1所示。已知电梯在t = 0时由静止开始上升,电梯的加速度a随时间t的变化如图2所示。如图1所示,一质量为M的乘客站在电梯里,电梯对乘客的支持力为F。根据a-t可以判断,力F大小不变,且F<Mg的时间段为
| A.1~8s内 | B.8~9s内 |
| C.15~16s内 | D.16~23s内 |
如图所示,水平桌面上放有一个盛着水的容器,水中有一个木球被细绳系在容器底部,若细绳断开,则木球在水中上升的过程中,水平桌面受到的压力大小将( )
| A.不变 | B.增大 | C.减小 | D.先增大后减小 |
为了研究超重与失重现象,某同学把一体重计放在电梯的地板上,并将一物体放在体重计上随电梯运动并观察体重计示数的变化情况。下表记录了几个特定时刻体重计的示数 (表内时间不表示先后顺序) 若已知t0时刻电梯静止,则:
| 时间 | t0 | t1 | t2 | t3 |
| 体重计示数(kg) | 45.0 | 50.0 | 40.0 | 45.0 |
B.t1和t2时刻物体的质量并没有发生变化,但所受重力发生了变化
C.t1和t2时刻电梯运动的方向一定相反
D.t3时刻电梯可能向上运动
某同学用测力计研究在竖直方向运行的电梯运动状态.他在地面上用测力计测量砝码的重力,示数为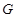 ;他在电梯中用该测力计仍测量同一砝码的重力,发现测力计的示数为0.9
;他在电梯中用该测力计仍测量同一砝码的重力,发现测力计的示数为0.9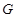 ,由此判断此时电梯的运动状态可能是:
,由此判断此时电梯的运动状态可能是:
| A.加速上升 | B.减速下降 | C.减速上升 | D.匀速下降 |
如图所示,一人站在电梯中的体重计上,随电梯一起运动。下列各种情况中,体重计的示数最大的是( )
| A.电梯匀减速上升,加速度的大小为 1.0 m/s2 |
| B.电梯匀加速上升,加速度的大小为 1.0 m/s2 |
| C.电梯匀减速下降,加速度的大小为 0.5 m/s2 |
| D.电梯匀加速下降,加速度的大小为 0.5 m/s2 |
压敏电阻的阻值会随所受压力的增大而减小,一同学利用压敏电阻设计了判断升降机运动状态的装置,如图甲所示,将压敏电阻平放在升降机内,受压面朝上,在上面放一物体m,升降机静止时电流表示数为I0。某过程中电流表的示数如图乙所示,则在此过程中 
| A.物体处于失重状态 |
| B.升降机一定向下做匀加速运动 |
| C.升降机一定向上做匀加速运动 |
| D.升降机可能向下做匀减速运动 |
电梯的顶部挂有一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10N,在某时刻电梯中的人观察到弹簧秤的示数变为8N,关于电梯的运动,以下说法正确的是(取g=10 m/s2) ( )
| A.电梯可能向上加速运动,加速度大小为2m/s2 |
| B.电梯可能向下加速运动,加速度大小为2m/s2 |
| C.电梯可能向上减速运动,加速度大小为2m/s2 |
| D.电梯可能向下减速运动,加速度大小为2m/s2 |
下列几种情况中,升降机绳索最不容易断的是( )
| A.以很大速度匀速上升 | B.上升时以很大的加速度减速 |
| C.以很小速度匀速下降 | D.下降时以很大的加速度减速 |
某同学站在观光电梯地板上,用加速度传感器记录了电梯由静止开始运动的加速度随时间变化情况,以竖直向上为正方向。根据图像提供的信息,可以判断下列说法中正确的是( )
| A.在5s~15s内,观光电梯在加速上升,该同学处于超重状态 |
| B.在15s~25s内,观光电梯停了下来,该同学处于平衡状态 |
| C.在25s~35s内,观光电梯在减速上升,该同学处于失重状态 |
| D.在t=35s时,电梯的速度为0 |
