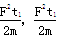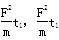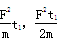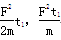右图为蹦极运动的示意图。弹性绳的一端固定在 点,另一端和运动员相连。运动员从
点,另一端和运动员相连。运动员从 点自由下落,至
点自由下落,至 点弹性绳自然伸直,经过合力为零的
点弹性绳自然伸直,经过合力为零的 点到达最低点
点到达最低点 ,然后弹起。整个过程中忽略空气阻力。分析这一过程,下列表述正确的是.
,然后弹起。整个过程中忽略空气阻力。分析这一过程,下列表述正确的是.
A.经过 点时,运动员的速率最大 点时,运动员的速率最大 |
B.经过 点时,运动员的速率最大 点时,运动员的速率最大 |
C.从 点到 点到 点,运动员的加速度增大 点,运动员的加速度增大 |
D.从 点到 点到 点,运动员的加速度不变 点,运动员的加速度不变 |
如图所示,一辆有动力驱动的小车上有一水平放置的弹簧,其左端固定在小车上,右端与一小球相连,设在某一段时间内小球与小车相对静止且弹簧处于压缩状态,若忽略小球与小车间的摩擦力,则在此段时间内小车可能是 ( )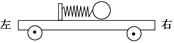
| A.向右做加速运动 | B.向右做减速运动 |
| C.向左做加速运动 | D.向左做减速运动 |
在设计水平面内的火车轨道的转变处时,要设计为外轨高、内轨低的结构,即路基形成一外高、内低的斜坡(如图所示)。内、外两铁轨间的高度差在设计上应考虑到铁轨转弯的半径和火车的行驶速度大小。若某转弯处设计为当火车以速率v通过时,内、外两侧铁轨所受轮缘对它们的压力均恰好为零。车轮与铁轨间的摩擦可忽略不计,则下列说法中正确的是
| A.当火车以速率v通过此弯路时,火车所受重力与铁轨对其支持力的合力提供向心力 |
| B.当火车以速率v通过此弯路时,火车所受各力的合力沿路基向下方向 |
| C.当火车行驶的速率大于v时,内侧铁轨对车轮的轮缘施加压力 |
| D.当火车行驶的速率小于v时,内侧铁轨对车轮的轮缘施加压力 |
有一质量为m的小木块,由碗边滑向碗底,碗的内表面是半径为R的圆弧,由于摩擦力的作用,木块运动的速率不变,则木块:
| A.所受合外力大小不变,方向随时间不断改变 | B.运动的加速度恒定 |
| C.所受合外力为零 | D.运动的加速度为零 |
同一辆汽车以同样大小的速度先后开上平直的桥和凸形桥,在桥的中央处有( )
| A.车对两种桥面的压力一样大 | B.车对平直桥面的压力大 |
| C.车对凸形桥面的压力大 | D.无法判断 |
如图甲所示,质量为M的木板静止在光滑水平面上,一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板.滑块和木板速度随时间变化的图象如图乙所示,某同学根据图象作出如下一些判断,不正确的是( ) ?
?
| A.滑块与木板间始终存在相对运动? |
| B.滑块始终未离开木板? |
| C.滑块的质量大于木板的质量? |
| D.在t1时刻滑块从木板上滑出 |
将一个电动传感器接在计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示。某同学由此图线提供的信息做出了下列判断( )
| A.t=0.2s时摆球正经过最低点 |
| B.t=1.1s时摆球正经过最低点 |
| C.摆球摆动过程中机械能守恒 |
| D.摆球摆动的周期是T=1.2s |
如图,车厢内有一斜面,其倾角为θ=37°. 质量为m的小球随车一起向右作加速运动,当车加速度处于一些不同的值时,小球可在车上不同位置相对车静止,不计小球与车的一切摩擦,则斜面对小球的弹力N可能( )
)
A.等于 | B.等于2mg | C.等于 | D.等于 |