如图所示, 用绳索将重球挂在墙上,不考虑墙的摩擦。如果把绳的长度增加一些,则球对绳的拉力F1和球对墙的压力F2的变化情况是:
| A.F1增大,F2减小 | B.F1减小,F2增大 |
| C.F1和F2都减小 | D.F1和F2都增大 |
三个相同光滑硬杆的O端连接在一起但各自能绕O点自由转动,OABC始终构成一个正三棱锥,杆的另一端ABC始终成一个等边三角形且在同一水平面,现在锥内放一个小球,然后缓慢使锥角变大,直到三根杆水平,该过程中每根杆对小球的作用力将( )
| A.一直减小 | B.一直增大 | C.先减小后增大 | D.先增大后减小 |
如图所示,绳与杆均不计重力,承受力的最大值一定.A端用绞链固定,滑轮O在A点正上方(滑轮大小及摩擦均可忽略),B端吊一重物P,现施加拉力FT将B缓慢上拉(均未断),在杆达到竖直前( ) 
| A.绳子越来越容易断 | B.绳子越来越不容易断 |
| C.杆越来越容易断 | D.杆越来越不容易断 |
如图所示,均匀光滑球夹在竖直墙和长木板之间静止,长木板的下端为固定转动轴.将长木板从图示位置缓慢地转到水平位置的过程中,小球对竖直墙的压力F1大小和小球对长木板的压力F2大小的变化情况将是( )
| A.F1、F2都逐渐减小 |
| B.F1、F2都逐渐增大 |
| C.F1逐渐减小,F2都逐渐增大 |
| D.F1逐渐增大,F2都逐渐减小 |
如图所示,一光滑小球静止放置在光滑半球面的最底端,利用竖直放置的光滑挡板水平向右缓慢地推动小球,则在小球运动的过程中(该过程小球未脱离球面),木板对小球的推力F1、半球面对小球的支持力F2的变化情况正确的是:
| A.F1增大、F2减小 | B.F1增大、F2增大 |
| C.F1减小、F2减小 | D.F1减小、F2增大 |
半圆柱体M放在粗糙的水平地面上,其右端有固定放置的竖直挡板PQ,M与PQ之间放有一个光滑均匀的小圆柱体N,整个系统处于静止。如图所示是这个系统的纵截面图。若用外力F使PQ保持竖直并且缓慢地向右移动,在N落到地面以前,发现M始终保持静止。在此过程中,下列说法正确的是
| A.地面对M的摩擦力逐渐增大 |
| B.MN间的弹力先减小后增大 |
| C.PQ对N的弹力逐渐减小 |
| D.PQ和M对N的弹力的合力逐渐增大 |
如图所示,一遵循胡克定律的弹性轻绳,其一端O固定在天花板上,另一端C与静止在水平地面上的滑块A相连。B为紧挨绳的一固定不动且与竖直面垂直的光滑小钉,它到天花板的距离BO等于弹性绳的自然长度。当绳OC处于竖直位置时,滑块A对地面有压力作用。现用一水平力F作用于A,使之在地面上向右做直线运动,且在运动过程中绳一直处于弹性限度内。若滑块A与水平地面间有摩擦,且动摩擦因数恒定,那么关于滑块A所受滑动摩擦力大小的判断,下列说法中正确的是
| A.逐渐增大 | B.逐渐减小 | C.保持不变 | D.无法确定 |
如图所示,物体在水平力F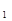 =15N、F
=15N、F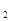 =6N的作用下,静止在水平面上,若F
=6N的作用下,静止在水平面上,若F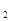 保持不变,当F
保持不变,当F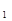 减小至10N时,物体受到的摩擦力( )
减小至10N时,物体受到的摩擦力( )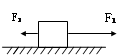
| A.增大至10N | B.变为9N |
| C.减小至6N | D.减小至4N |
如图所示,不计滑轮质量与磨擦,重物挂在滑轮下,绳A端固定将B端绳由B移到C或D(绳长不变)其绳上张力分别为TB,TC,TD,绳与竖直方向夹角θ分别为θB,θC,θD则 ( )
| A.TB>TC>TDθB<θC<θD |
| B.TB<TC<TDθB<θC<θD |
| C.TB=TC<TDθB=θC<θD |
| D.TB=TC=TDθB=θC=θD |
如图所示,小球用细绳系住放置在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,细绳上的拉力F和斜面对小球的支持力N将:
| A.N逐渐增大 | B.N逐渐减小 |
| C.F先增大后减小 | D.F逐渐减小 |