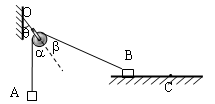
研究共点力合成时,使b弹簧按图示位置顺时针缓慢转动到竖直位置,此过程中保持橡皮条下端O点位置不变和弹簧a的方向不变, 则两弹簧弹力变化是
| A.a增大,b减小 |
| B.a减小,b增大 |
| C.a减小,b先增大后减小 |
| D.a减小,b先减小后增大 |
如右图所示,用绳索将重球挂在墙上,不考虑墙的摩擦.如果把绳的长度缩短一些,则球对绳的拉力F1和球对墙的压力F2的变化情况是:
| A.F1增大,F2减小 |
| B.F1减小,F2增大 |
| C.F1和F2都减小 |
| D.F1和F2都增大 |
如图所示,有一个直角支架 AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑,AO上套有小环P,OB上套有小环 Q,两环质量均为m,两环间由一根质量可忽略、不可伸展的细绳相连,并在某一位置平衡(如图),现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力N、摩擦力f和细绳上的拉力T的变化情况是: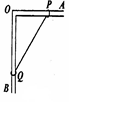
| A.N不变,T变大,f不变 | B.N不变,T变小,f变小 |
| C.N变小,T变大,f不变 | D.N变大,T变小,f变小 |
如图,轻绳的两端分别系在圆环A和小球B上,圆环A套在粗糙的水平杆上,现用水平力F将小球B缓慢地拉至虚线处,在此过程中A的位置操持不变,则环A对杆的摩擦力f 和压力N 如何变化:( )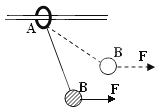
| A.f 不变,N 不变; |
| B.f 增大,N 不变; |
| C.f 增大,N 减小; |
| D.f 不变,N 减小; |
如右图所示,一圆环位于竖直平面内,圆环圆心处的一小球,OP、OQ为两根细绳,一端与球相连另一端固定在圆环上。OP呈水平,OQ与竖直方向成30º角,现保持小球位置不动,将圆环沿顺时针方向转过90º角,则在此过程中 ( )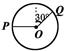
A.OP绳所受拉力增大 |
| B.OP绳所受拉力先增大后减小 |
| C.OQ绳所受拉力先减小后增大 |
| D.OQ绳所受拉力先增大后减小 |
如下图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工人及其装备的总重量为G,悬绳与竖直墙壁的夹角为α,悬绳对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,空中作业时工人与玻璃的水平距离为定值,则 
A. |
B. |
| C.在空中同一位置作业,当桶中的水不断减少,F1与F2同时减少 |
| D.若缓慢增加悬绳的长度,F1减小,F2增大 |
如图所示,物体m静止于倾斜角为θ的木板上,在θ缓慢从0°增大到90°的过程中,下列说法中正确的是 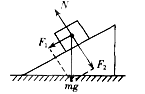
| A.物体所受的摩擦力逐渐增大 |
| B.物体对木板的压力逐渐增大 |
| C.物体所受的支持力逐渐减小 |
| D.物体所受摩擦力先增大后减小 |
如图用细绳悬挂一个小球,小球在水平拉力F的作用下从平衡位置P点缓慢地沿圆弧移动到Q点,在这个过程中,绳子拉力T和水平拉力F的大小变化情况是( )
| A.T不断增大,F不断减小 | B.T不断减小,F不断增大 |
| C.T与F都不断增大 | D.T与F都不断减小 |