一根轻质弹簧,竖直悬挂,原长为10 cm。当弹簧下端挂2.0 N的重物时,伸长1.0 cm;则当弹簧下端挂8.0 N的重物时,弹簧总长( )
| A.4.0 cm | B.14.0 cm | C.18.0 cm | D.8.0 cm |
在轻质弹簧下端悬挂一质量为0.1kg的物体,当物体静止后,弹簧伸长了0.01m,取g=10m/s2。该弹簧的劲度系数为
| A.1N/m | B.10N/m | C.100N/m | D.1000N/m |
质量为m的球置于倾角为θ的光滑斜面上,被与斜面垂直的光滑挡板挡着,如图所示。当挡板从图示位置缓缓作逆时针转动至水平位置的过程中,挡板对球的弹力
N1和斜面对球的弹力N2的变化情况是( )
| A.N1增大 | B.N1先减小后增大 | C.N2增大 | D.N2减小 |
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计。再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为
( )
| A.乙图读数F0—G,丙图读数F0+G |
| B.乙图读数F0+G,丙图读数F0—G |
| C.乙图读数F0,丙图读数F0—G |
| D.乙图读数F0—G,丙图读数F0 |
如图所示,小车上固定一弯折硬杆ABC,C端固定一质量为m的小球。已知α角恒定,当小车水平向左作变加速直线运动时,BC杆对小球的作用力的方向( )
| A.一定沿着杆向上 | B.一定竖直向上 |
| C.可能水平向左 | D.随加速度a的数值的改变而改变 |
如图所示,三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑它们与锲块间的动摩擦因数各不相同,致使第一小木块加速下滑,第二小木块匀速下滑,第三小木块以初速υ0减速下滑.则在下滑过程中,锲块对地面的压力N1、N2、N3之间的关系为
| A.N1=N2=N3 |
| B.N1>N2>N3 |
| C.N2>N1>N3 |
| D.N3>N2>N1? |
探究弹力和弹簧伸长的关系时,在弹性限度内,悬挂12 N的重物时,弹簧长度为0.16m;悬挂20 N的重物时,弹簧长度为0.20 m,则弹簧的劲度系数k为( )
| A.75 N/m | B.100 N/m | C.200 N/m | D.250 N/m |
下列关于力的说法正确的是( )
| A.只有直接接触的物体间才有力的作用 |
| B.重力就是地球对物体的吸引力 |
| C.相互接触的物体之间才能产生弹力 |
| D.只有施力物体却没有受力物体的力是不存在的 |


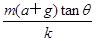 B.
B.
 D.
D.