甲、乙两物体先后从同一地点出发,沿一条直线运动,它们的v-t图象如图所示,由图可知( )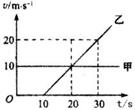
| A.甲比乙运动得快,且早出发,所以乙追不上甲 |
| B.t=20s时,乙追上了甲 |
| C. t=20s时,甲与乙间的间距最大 |
| D.在t=20s之前,甲比乙运动得快,t=20s之后乙比甲运动得快 |
如图,甲、乙两个物体相距x=7m,物体甲在水平拉力和摩擦力作用下,正以v1=4 m/s的速度向右匀速运动,而物体乙此时的速度v2=10m/s,由于摩擦力作用向右匀减速运动,加速度大小a=2 m/s2,那么物体甲追上乙所用的时间为( )
| A.7s | B.8s | C.9s | D.10s |
如图所示是做直线运动的甲、乙两物体的位移时间(s-t)图象,下列说法中错误的是 ( )
| A.甲启动的时刻比乙早t1 |
| B.当 t = t2时,两物体相遇 |
| C.当t = t2时,两物体相距最远 |
| D.当t = t3时,两物体相距S1 |
两个物体甲和乙,从某地点同时沿同一方向作直线运动,其v-t 图线如图所示,则以下判断正确的是( )
| A.在2秒末,甲和乙相遇 |
| B.在4 秒末,甲和乙相遇 |
| C.开始运动2秒以后,乙的速度比甲的速度大 |
| D.在开始运动2秒内,甲的平均速度大于乙的平均速度 |
汽车甲沿着平直的公路以速度v0做匀速直线运动,当它经过某处的同时,该处有汽车乙开始作初速度为零的匀加速直线运动去追赶甲车,根据已知条件()
| A.可求出乙车追上甲车时乙车的速度 |
| B.可求出乙车追上甲车时乙车的路程 |
| C.可求出乙车从开始起动到追上甲车时所用的时间 |
| D.不能求出上述三者中的任何一个. |
甲、乙两物体由同一位置出发沿一直线运动,其速度—时间图象如图所示,下列说法正确的是( )
| A.甲做匀速直线运动,乙做匀变速直线运动 |
| B.两物体两次相遇的时刻分别是在2 s末和6 s末 |
| C.乙在头2 s内做匀加速直线运动,2 s后做匀减速直线运动 |
| D.2 s后,甲、乙两物体的速度方向相反 |
某同学根据自己的生活体验设置了这样一个问题:甲物体沿直线MN做匀速直线运动,速度为v1. P点到MN的垂直距离为s,如图所示. 乙物体由P点开始运动,要追上甲物体. 设乙物体可沿任意方向运动且速度大小始终是v2. 已知v2>v1. 某时刻当甲位于直线MN上的F点时,乙物体由P点开始运动,问,乙物体能否追上甲物体?哪种追赶方式用时最短?同学们通过分析以后得出以下几种不同的观点,你认为正确的是( )
| A.乙物体沿PFN的路线追赶甲物体时,用时最短 |
| B.乙物体追赶过程中,保持其速度的方向总是指向甲物体,这样运动方式用时最短 |
| C.通过计算,使乙物体沿某直线PE运动,到达直线MN时正好与甲物体相遇,这种方式用时最短 |
| D.在A、B、C三种追赶方式中,乙物体都能追上甲物体 |
两辆车沿着平直公路往同一方向行驶,某时刻恰好经过同一位置,此时A以4m/s的速度继续匀速向前,而B以10m/s的速度开始刹车,加速度大小为2m/s2。那么它们再次遇上所经过的时间为( )
| A.5s | B.6s | C.6.25s | D.6.5s |
两列火车相向而行,第一列火车的速度大小为36km/h,第二列火车为54km/h。第一列火车上的乘客测出第二列火车从他旁边通过所用的时间为5s。以下结论正确的是( )
| A.两列火车的长度之和为125m |
| B.第二列火车的长度是125m |
| C.第二列火车的长度是75m |
| D.由于第一列火车的长也未知,故无法求出第二列火车的长 |