汽车甲沿着平直的公路以速度v0做匀速直线运动,当它路过某处的同时,汽车乙从此处开始以加速度a做初速度为零的匀加速直线运动去追赶汽车甲,根据上述已知条件( )
| A.可求出乙车追上甲车时,乙车的速度 |
| B.可求出乙车追上甲车时,乙车走的路程 |
| C.可求出乙车从开始运动到追上甲车时,乙车运动的时间 |
| D.不能求出上述三者中任何一个 |
甲乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s2>s1).初始时,甲车在乙车前方s0处( )
| A.若s0=s1+s2,两车不会相遇 |
| B.若s0<s1,两车相遇2次 |
| C.若s0=s1,两车相遇1次 |
| D.若s0=s2,两车相遇1次 |
甲?乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图中(如图),直线a?b分别描述了甲?乙两车在0~20 s的运动情况.关于两车之间的位置关系,下列说法正确的是( )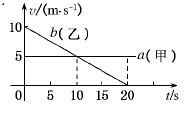
| A.在0~10 s内两车逐渐靠近 |
| B.在10~20 s内两车逐渐远离 |
| C.在5~15 s内两车的位移相等 |
| D.在t="10" s时两车在公路上相遇 |
甲乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示.两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能的是( )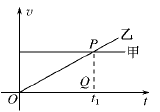
| A.t′=t1,d=S | B.t′= t1,d= t1,d= S S |
C.t′= t1,d= t1,d= S S | D.t′= t1,d= t1,d=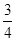 S S |
小李讲了一个龟兔赛跑的故事,按照小李讲的故事情节,兔子和乌龟的位移图象如图8所示,由图可知 ( )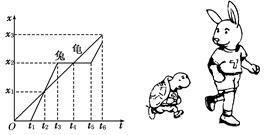
| A.兔子和乌龟是同时同地出发 |
| B.兔子和乌龟在比赛途中相遇过两次 |
| C.乌龟做的是匀速直线运动,兔子是沿着折线跑的 |
| D.乌龟先通过预定位移到达终点 |
(2011年福建联考)甲、乙两车某时刻由同一地点沿同一方向开始做直线运动,若从该时刻开始计时,得到两车的位移图象如图1-3-8所示,则下列说法正确的是( )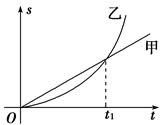
图1-3-8
| A.t1时刻甲车从后面追上乙车 |
| B.t1时刻两车相距最远 |
| C.t1时刻两车的速度刚好相等 |
| D.从0时刻到t1时刻的时间内,两车的平均速度相等 |
在一条平直的公路上,甲车由静止开始以加速度a做匀加速运动,在加速度阶段,与同向匀速行驶的乙车在公路上相遇两次.已知第一次相遇时甲车的速度不为零,乙车的速度为v,下列判断正确的是( )
| A.甲车开始运动时,乙车一定在甲车前面 |
B.甲车开始运动时,甲、乙两车的距离一定小于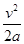 |
| C.第一次相遇时,甲车速度一定大于v |
| D.第二次相遇时,甲车速度一定小于2v |
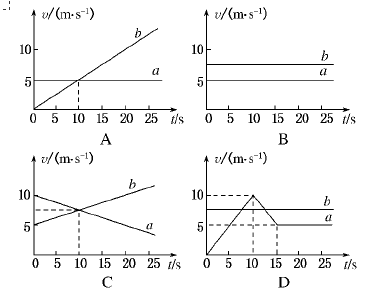
一辆警车在平直的公路上以20 m/s的速度巡逻,突然接到报警,在前方不远处有歹徒抢劫,该警车要尽快赶到出事地点且到达出事地点时的速度也为20 m/s,有三种行进方式:a为一直匀速直线运动;b为先减速再加速;c为先加速再减速,则 ( )
| A.a种方式先到达 | B.b种方式先到达 |
| C.c种方式先到达 | D.条件不足,无法确定 |