Question

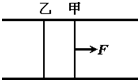（2003?天津）两根平行的金属导轨，固定在同一水平面上，磁感B=0.50T的匀强磁场与导轨所在平面垂直，导轨的电阻很小，可不计．导轨间的距离l=0.20m．两根质量均为m=0.10kg的平行杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的为电阻R=0.50Ω，在t=0时刻，两杆都处于静止状态．现有一与导轨平行，大小为0.20N的作用于金属杆甲上，使金属杆在导轨上滑动．经过t=0.5s，金属杆甲的加速度a=1.37m/s²，问此时两金属杆的速度各为多少？

Answer 1

分析：根据磁通量定义，法拉第电磁感应定律与动量定理，即可求解．

解答：解：设任一时刻t两金属杆甲、乙之间的距离为x，速度分别为v₁和v₂，
经过很短的时间△t，杆甲移动距离v₁△t，杆乙移动距离v₂△t，
回路面积改变
△S=（（x-v₂△t）+v₁△t）+t-lx=（v₁-v₂）l△t
由法拉第电磁感应定律，回路中的感应电动势E=B

△S

△t

回路中的电流i=

E

2R

 
杆甲的运动方程F-Bli=ma由于作用于杆甲和杆乙的安培力总是大小相等，方向相反，
所以两杆的动量（t=0时为0）等于外力F的冲量F₁=mv₁+mv₂
联立以上各式解得v1=

1

2

(

F1

m

+

2R

B2F

(F-ma))  
v2=

1

2

(

F1

m

-

2R

B2I2

(F-ma))
代入数据得v₁=8.15m/s
v₂=1.85m/s
答：两金属杆的速度各为v₁=8.15m/s；v₂=1.85m/s．

点评：考查感应电流产生的条件，法拉第电磁感应定律与动量定理的应用，注意其公式的矢量性．