题目内容
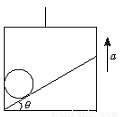
 升降机中的斜面和竖直面间放一个质量为10kg的小球,斜面的倾角为30°,如图所示.(不计摩擦,g取10m/s2)
升降机中的斜面和竖直面间放一个质量为10kg的小球,斜面的倾角为30°,如图所示.(不计摩擦,g取10m/s2)(1)当升降机静止时,求斜面所受压力;
(2)当升降机由静止匀加速上升时,第1s内的位移为2m.求斜面受的压力.
分析:(1)当升降机时小球也静止,对小球受力分析后应用平衡条件列式求出斜面对小球的支持力,再根据牛顿第三定律求出斜面所受的压力.
(2)当升降机由静止匀加速上升时,已知位移和时间,先由位移公式x=
at2,求出加速度,再根据牛顿第二定律求解.
(2)当升降机由静止匀加速上升时,已知位移和时间,先由位移公式x=
| 1 |
| 2 |
解答: 解:(1)取小球为研究对象,小球受3个力:斜面对小球的支持力 N,挡板对小球的支持力F,重力G,如图所示:
解:(1)取小球为研究对象,小球受3个力:斜面对小球的支持力 N,挡板对小球的支持力F,重力G,如图所示:
由力的平衡条件得:
N=
=
N
则根据牛顿第三定律得:斜面所受的压力大小为N′=N=
N
(2)由x=
at2得 a=4m/s2
根据牛顿第二定律得 N′cosθ-mg=ma
解得 N′=
N
根据牛顿第三定律得:斜面所受的压力大小为N″=N′=
N
答:
(1)当升降机静止时,斜面所受压力为
N;
(2)当升降机由静止匀加速上升时,第1s内的位移为2m.斜面受的压力为
N.
 解:(1)取小球为研究对象,小球受3个力:斜面对小球的支持力 N,挡板对小球的支持力F,重力G,如图所示:
解:(1)取小球为研究对象,小球受3个力:斜面对小球的支持力 N,挡板对小球的支持力F,重力G,如图所示:由力的平衡条件得:
N=
| G |
| cos30° |
200
| ||
| 3 |
则根据牛顿第三定律得:斜面所受的压力大小为N′=N=
200
| ||
| 3 |
(2)由x=
| 1 |
| 2 |
根据牛顿第二定律得 N′cosθ-mg=ma
解得 N′=
280
| ||
| 3 |
根据牛顿第三定律得:斜面所受的压力大小为N″=N′=
280
| ||
| 3 |
答:
(1)当升降机静止时,斜面所受压力为
200
| ||
| 3 |
(2)当升降机由静止匀加速上升时,第1s内的位移为2m.斜面受的压力为
280
| ||
| 3 |
点评:此题对小球进行受力分析,运用力的合成或分解结合共点力平衡条件解决问题.

练习册系列答案
相关题目