题目内容
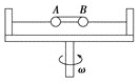
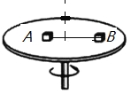
【题目】如图所示,在匀速转动的水平圆盘上,在圆心两侧、沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20cm,rB=30cm,A、B与盘间最大静摩擦力均为重力的k=0.4倍,现极其缓慢的增加转盘的角速度,(g取10m/s2)试求:
(1)当细线上开始出现张力时,圆盘的角速度ω0;
(2)当细线出现张力后,A所受摩擦力最小时,圆盘的角速度ω1。
【答案】(1)![]() (2)
(2)![]()
【解析】
当细线上开始出现张力时,B的摩擦力达到最大静摩擦力,由牛顿第二定律求出圆盘的角速度;当细线出现张力后,A所受摩擦力最小时,分别对A、B由牛顿第二定律求出圆盘的角速度;
解:(1) 当细线上开始出现张力时,B的摩擦力达到最大静摩擦,此时
![]()
解得![]()
(2)当![]() 时,
时,
对B: ![]()
对A: ![]()
解得:![]()
当![]() 时,
时,
解得![]()

练习册系列答案
相关题目