题目内容
如图所示，一小球A的质量为m，带电量为一g，用长为L 的绝缘轻杆跟固定小球B相连接，绝缘轻杆可绕小球B无摩擦转动．整个装置处于水平向右的匀强电场中，轻杆从图中竖直位置由静止释放，转过的最大角度为127，（sin37°=0.6，cos37°=0.8）．求：（1）匀强电场的场强大小E；
（2）轻杆转过90时的速度大小．
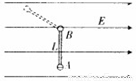
【答案】分析：（1）对整个过程运用动能定理，抓住动能变化为零，求出匀强电场的场强E．
（2）根据动能定理求出轻杆转过90°时球的速度大小．
解答：解：（1）根据题意，由动能定理得
qELcos37°-mg（L+Lsin37°）=0
解得场强 E=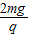
（2）设轻杆转过90°时小球A的速度为v，由动能定理有
qEL-mgL=
mv2-0
解得 v=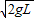
答：
（1）匀强电场的场强大小E为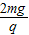
；
（2）轻杆转过90时的速度大小为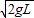
．
点评：本题考查动能定理的应用能力，对于涉及力在空间效果的过程，往往运用动能定理求解．
（2）根据动能定理求出轻杆转过90°时球的速度大小．
解答：解：（1）根据题意，由动能定理得
qELcos37°-mg（L+Lsin37°）=0
解得场强 E=
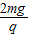
（2）设轻杆转过90°时小球A的速度为v，由动能定理有
qEL-mgL=
mv2-0解得 v=
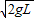
答：
（1）匀强电场的场强大小E为
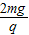；（2）轻杆转过90时的速度大小为
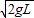．点评：本题考查动能定理的应用能力，对于涉及力在空间效果的过程，往往运用动能定理求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一小球A点由静止自由下落，到B点时与弹簧接触，到C点时弹簧被压缩到最短．若不计弹簧质量和空气质量，在小球由A→B→C的过程中，若仅以小球、地球为系统，且取地面为参照面，则（ ）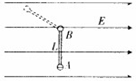
如图所示，一小球A的质量为m，带电量为一g，用长为L 的绝缘轻杆跟固定小球B相连接，绝缘轻杆可绕小球B无摩擦转动．整个装置处于水平向右的匀强电场中，轻杆从图中竖直位置由静止释放，转过的最大角度为1270，（sin37°=0.6，cos37°=0.8）．求：
两个小球固定在一根长为1m的杆的两端，杆绕O点逆时针旋转，如图所示，当小球A的速度为3m/s时，小球B的速度为12m/s．则小球B到转轴O的距离是（ ）
光源之间的距离为L，今将小球以水平速V0向右抛出。