Question

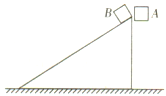
【题目】如图所示，粗糙的地面上放着一个质量M＝1.5kg的斜面，斜面部分光滑，底面与地面的动摩擦因数μ＝0.2，倾角θ＝37°，在固定在斜面的挡板上用轻质弹簧连接一质量m＝0.5kg的小球，弹簧劲度系数k＝200N/m，现给斜面施加一水平向右的恒力F，使整体向右以a＝1 m/s2的加速度匀加速直线运动．(已知sin37°＝0.6、cos37°＝0.8，g＝10m/s2)

(1)求F的大小；

(2)求出弹簧的形变量及斜面对小球的支持力大小．

Answer 1

【答案】（1）6N（2）0.017m；3.7N

【解析】试题分析：（1）以整体为研究对象，列牛顿第二定律方程

（2）对小球受力分析，水平方向有加速度，竖直方向受力平衡

解：（1）整体以a 匀加速向右运动，对整体应用牛顿第二定律：

F﹣μ（M+m）g=（M+m）a

得F=6N

（2）设弹簧的形变量为x，斜面对小球的支持力为FN

对小球受力分析：

在水平方向：Kxcosθ﹣FNsinθ=ma

在竖直方向：Kxsinθ+FNcosθ=mg

解得：x=0.017m

FN=3.7N

答：（1）F的大小6N；

（2）弹簧的形变量0.017m

斜面对小球的支持力大小3.7N