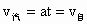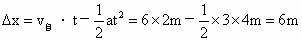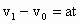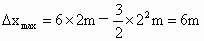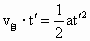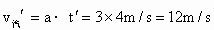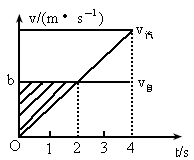题目内容
一小汽车从静止开始以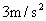 的加速度行驶,恰有一自行车以6m/s的速度从车边匀速驶过.
的加速度行驶,恰有一自行车以6m/s的速度从车边匀速驶过.
(1)汽车从开动后在追上自行车之前经多长时间后两者相距最远?此时距离是多少?
(2)什么时候追上自行车,此时汽车的速度是多少?
答案:2s,6m;4s,12m/s
解析:
解析:
|
对设问 (1)解法Ⅰ:汽车开动后速度由零逐渐增大,而自行车速度是定值,当汽车的速度还小于自行车的速度时,两者距离越来越大,当汽车的速度大于自行车的速度时,两者距离越来越小.所以当两车的速度相等时,两车之间距离最大. 有
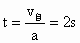 . .
解法Ⅱ:利用相对运动求解. 以自行车为参考系,汽车追上自行车之前初速 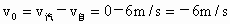 ,加速度 ,加速度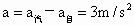 . .
汽车远离自行车减速运动 (与自行车对地运动方向相反),当末速为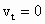 时,相对自行车最远. 时,相对自行车最远.
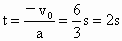 . .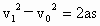 , ,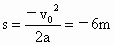 . .
负号表示汽车比自行车落后. 解法Ⅲ:极值法. 设汽车在追上自行车之前经时间 t相距最远.
利用二次函数求极值条件知 当 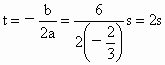 时, 时,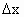 最大, 最大,
故
对设问 (2)汽车追上自行车时,两车位移相等.
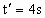 , ,
解法Ⅳ:如下图所示,作出 v-t图
(1) 设相遇前ts两车速度相等,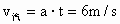 ,即3t=6,解得t=2s时两车相距最远. ,即3t=6,解得t=2s时两车相距最远.
两车的位移差 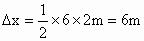 . .
(2) 由图知,t=2s以后,若两车位移相等,即v-t图象与时间量所夹的“面积”相等.由几何关系知,相遇时间为 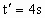 ,此时 ,此时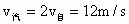 . .
注意:(1) 本题采用了多种解法,如综合法,相对运动法、极值法、图象法等,各有特色,这体现了对同一问题的理解角度不同,解法不同.(2) 在解决运动学问题时,在解题方法上可以从公式图象等方面、多角度考虑问题,利用图象解决问题能把抽象的物理过程变得直观形象,易于接受,且计算过程相对简化. |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目