��Ŀ����
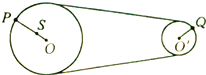
����Ŀ����ͼ��ʾ,��ˮƽ�������������絼��MN��PQ��������Ϊd����ǿ�ų���ֱ�ڵ������ڵ�ƽ������Ÿ�Ӧǿ�ȵĴ�СΪB��������ȫ��ͬ�Ľ�����1��2���һ���ľ���ڿ����ڵ����ϣ����뵼�촹ֱ�����ǵĵ����ΪR�������뵼��Ӵ����ã�������費�ƣ������˵�Ħ�����ơ���1�Գ��ٶ�v0�����2��Ϊʹ���˲����������2�̶��벻�̶���������£�����ڷ�����ʱ�����پ���֮��Ϊ��

A. 1:1 B. 1:2 C. 2:1 D. 1:1
���𰸡�C
��������������1��2�����̶�ʱ��ϵͳ�����غ���������Ϊ���������У�mv0=2mv����ã�v=![]() ��
��
���Ҳ�ˣ�����Ԫ����������Ϊ�������ݶ����������У���F��t=��m��v��
����F=BIL= ![]() ��
��
��![]() ��t=��m��v��
��t=��m��v��
��![]() ��
��
��ã�l1l2=![]() ����AB��ľ�����СΪx=
����AB��ľ�����СΪx=![]() ��
��
����2�̶���������������Ϊ�������ݶ����������У���F��t=��m��v��
����F=BIL=B![]() L��
L��
�ʣ���![]() ��t=��m��v��
��t=��m��v��
��![]() =mv0��
=mv0��
��ã�l=![]() ����AB��ľ�����СΪx��=
����AB��ľ�����СΪx��=![]() ��
��
��x��x��=1:2��
��ABD����C��ȷ��
��ѡ��C��

��ϰ��ϵ�д�
�����Ŀ