Question

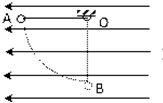如图所示，空间存在水平向左的匀强电场，一根长为L且不可伸长的轻质细线的一端固定于悬点O，另一端连接一个质量为m的带正电的小球．平衡时细线与竖直方向的夹角α=30°．现将小球拉到A处使细线处于水平且伸直的状态，由静止释放小球，求小球运动到悬点O的正下方B时小球对细线的拉力．（重力加速度为g）

Answer 1

分析：小球静止时，由平衡条件求出电场力的大小．小球所受的电场力水平向右，由静止释放小球，根据动能定理求出小球到达B点时的速度，根据牛顿第二定律求解细线的拉力，从而得到小球对细线的拉力．

解答：解：小球在平衡点受力分析：电场力 F_电=qE=mgtan30°；
小球从A到B的过程，由动能定理：mgL-qEL=

1

2

mv2；
在最低点受力分析得：T-mg=m

v2

L

得出绳子对球拉力T=（3-

3

3

）mg
由牛顿第三定律：球对绳子拉力T=（3-

3

3

）mg，方向向下．
答：小球运动到悬点O的正下方B时小球对细线的拉力大小为（3-

3

3

）mg，方向向下．

点评：本题是带电物体在电场中圆周运动问题，动能定理和向心力结合是常用的解题方法．常见的题型．对于多过程的问题可能多次应用动能定理求解问题．