��Ŀ����
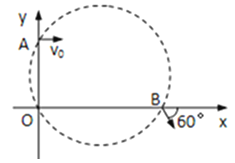
����Ŀ����ͼ��ʾ,�뾶ΪR�İ�Բ�������ڴ��ڴ�ֱֽ�����ڵ���ǿ�ų�,�Ÿ�Ӧǿ�ȴ�СΪB,Բ����P����Բ��O�����ߴ�ֱ��ֱ��MN,P�����һ����Դ,����ֽ���ڸ���������ȷ�������ԭ�Ӻ�![]() ��
��![]() ,
,![]() ������Ϊv,
������Ϊv, ![]() ������Ϊ
������Ϊ![]() ,��PO�������
,��PO�������![]() ǡ�ô�N���뿪�ų�,����ԭ�Ӻ˼������ü�ԭ�Ӻ˵�����,ȡsin53��=0.8,cos53��=0.6��
ǡ�ô�N���뿪�ų�,����ԭ�Ӻ˼������ü�ԭ�Ӻ˵�����,ȡsin53��=0.8,cos53��=0.6��

(1)��ԭ�Ӻ�![]() �ıȺ�
�ıȺ�![]() (��B��v��R��ʾ)�����P�㵽�߽�MN�����ʱ�䣻
(��B��v��R��ʾ)�����P�㵽�߽�MN�����ʱ�䣻
(2)����һԭ�Ӻ�![]() �Ĺ켣ǡ����ON���е�A����,��
�Ĺ켣ǡ����ON���е�A����,��![]() ���ӵ�������a��
���ӵ�������a��
(3)��ֱ��MN�ϰ�װ������,�������r������ӵ�,�������ԭ�Ӻ˵��������������γɵ�������֪����ԴP��λʱ���ڷ���n������,����![]() ռ40%,
ռ40%,![]() ռ60%,���ȶ���ͨ������r�ĵ�����С��(��֪���ӵĵ����Ϊe)
ռ60%,���ȶ���ͨ������r�ĵ�����С��(��֪���ӵĵ����Ϊe)
���𰸡�(1) ![]() ;
; ![]() (2)
(2) ![]() (3)
(3) ![]()
��������
��1��������֪����������Ӧ���˶��켣ͼ�����ݼ��ι�ϵ�����С��Բ�Ľ⣬�ٸ���![]() �����̵��˶�ʱ�䣻��2��������֪����������Ӧ���˶��켣ͼ�����ݼ��ι�ϵ����˶��뾶���������������ṩ����������Ⱥɣ��������������a����3��������֪����������Ӧ���˶��켣ͼ�����ݼ��ι�ϵ�����Ӧ�ĽǶȣ��Ӷ�������ӿ��ܳ�����ķ�Χ���ٸ��ݵ����Ķ���ʽ��������ı���ʽ��
�����̵��˶�ʱ�䣻��2��������֪����������Ӧ���˶��켣ͼ�����ݼ��ι�ϵ����˶��뾶���������������ṩ����������Ⱥɣ��������������a����3��������֪����������Ӧ���˶��켣ͼ�����ݼ��ι�ϵ�����Ӧ�ĽǶȣ��Ӷ�������ӿ��ܳ�����ķ�Χ���ٸ��ݵ����Ķ���ʽ��������ı���ʽ��
��1������֪�����ã�Բ���˶��İ뾶ΪR����![]() ����
����![]()
��OP��̣�������Ӧ��Բ�Ľ�Ҳ��С����Ӧ��ʱ��Ҳ�������ͼ��ʾ��
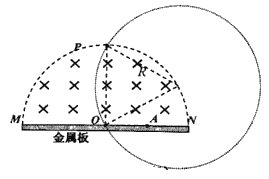
�ɼ��ι�ϵ�ã�Բ�Ľ�Ϊ![]() ���˶�������Ϊ
���˶�������Ϊ![]()
���˶���ʱ��Ϊ![]()
��2����Բ���˶��뾶Ϊ![]() ����ͼ��ʾ����
����ͼ��ʾ����
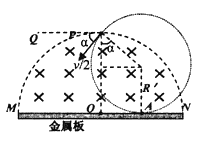
�ɼ��ι�ϵ�ã�![]()
��ã�![]()
��Y���ӵ�����Ϊ![]() �������Ϊ
�������Ϊ![]()
��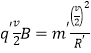 ����ã�
����ã�![]()
������ã�![]() ����
����![]() �������a=15
�������a=15
��3����Y���ӣ������ӳ��ٶȷ���������PQ����н�Ϊ![]() ����ͼ��ʾ��
����ͼ��ʾ��

��֪�켣ǡ����A���У���![]()
�������ݽ�ã�![]() ����ã�
����ã�![]()
�ɼ��ι�ϵ��Y������![]() ��Χ�ڳ����ܵ��������
��Χ�ڳ����ܵ��������
��λʱ��������Y������Ϊ![]()
�ɼ��ι�ϵ��Y������![]() ��Χ�ڳ����ܵ��������
��Χ�ڳ����ܵ��������
��λʱ��������Y������Ϊ![]()
ͨ������r�ϵĵ���![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�