题目内容
 一列简谐横波沿x轴正方向传播,某时刻(设t=0)波传播到x轴上的B质点,在它左边的A质点正在负最大位移处,如图所示,在t=0.6s时,质点A第二次出现在正的最大位移处,则( )
一列简谐横波沿x轴正方向传播,某时刻(设t=0)波传播到x轴上的B质点,在它左边的A质点正在负最大位移处,如图所示,在t=0.6s时,质点A第二次出现在正的最大位移处,则( )| A、该简谐波的波速等于10m/s | B、t=0.6s时,质点C在平衡位置处且向上运动 | C、当质点E第一次出现在正最大位移处时,质点B恰好在平衡位置且向下运动 | D、此波通过宽度为2m的孔时能发生明显衍射现象 |
分析:根据波动图象得出波长的大小,结合质点振动的周期等于波的周期,求出波速的大小.根据波速和时间求出t=0.6s时波传播的距离,确定质点C所处的位置,从而确定其振动情况.根据B、E之间的距离与波长的关系,确定其振动的关系.
解答:解:A、由意义可知,经过
T,质点A第二次出现在正的最大位移处,即
T=0.6s,则T=0.4s.波长λ=0.02m,则波速v=
=
=0.05m/s.故A错误.
B、经过t=0.6s时,波向前传播的距离x=vt=0.03m,知道C在平衡位置向上运动.故B正确.
C、E和B之间的距离等于
λ,当质点E第一次出现在正最大位移处时,质点B处于负的最大位移处.故C错误.
D、因为波长的大小为0.02m,比孔的大小小得多,不能发生明显的衍射.故D错误.
故选:B.
| 3 |
| 2 |
| 3 |
| 2 |
| λ |
| T |
| 0.02 |
| 0.4 |
B、经过t=0.6s时,波向前传播的距离x=vt=0.03m,知道C在平衡位置向上运动.故B正确.
C、E和B之间的距离等于
| 3 |
| 2 |
D、因为波长的大小为0.02m,比孔的大小小得多,不能发生明显的衍射.故D错误.
故选:B.
点评:解决本题的关键知道质点振动的周期等于波的周期,知道振动和波动的联系.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
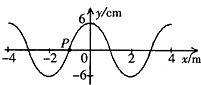 一列简谐横波沿x轴传播,t=0时刻的波形如图所示,此刻质点P正沿Y轴正方向振动.在t=0.02s时刻,质点P第一次达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时刻的波形如图所示,此刻质点P正沿Y轴正方向振动.在t=0.02s时刻,质点P第一次达正向最大位移处,由此可知( )| A、此波沿x轴正方向传播 | B、此波的传播速度为50m/s | C、从t=0起经0.04s质点P沿传播方向移动了2m | D、质点P的振动方程为y=6sin25πt(cm) |
 一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图7-2所示.在t2=0.6s时,质点A第二次出现在正的最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t1=0时波传播到x轴上的质点B,在它左边的质点A恰好位于负最大位移处,如图7-2所示.在t2=0.6s时,质点A第二次出现在正的最大位移处,则( )| A、该简谐波的波速等于10 m/s | B、t2=0.6 s时,质点C在平衡位置处且向下运动 | C、t2=0.6 s时,质点C在平衡位置处且向上运动 | D、当质点D第一次出现在正最大位移处时,质点B恰好在平衡位置且向下运动 |

 (2008?绵阳模拟)一列简谐横波沿x 轴正方向以v=4m/s的速度传播,在某一时刻的波形如图所示,从图示时刻开始,经过△t=1s,x轴上的某质点P,处在x 轴下方且向+y 方向运动,则质点P距离y 轴可能是( )
(2008?绵阳模拟)一列简谐横波沿x 轴正方向以v=4m/s的速度传播,在某一时刻的波形如图所示,从图示时刻开始,经过△t=1s,x轴上的某质点P,处在x 轴下方且向+y 方向运动,则质点P距离y 轴可能是( ) 一列简谐横波沿x轴传播.T=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )
一列简谐横波沿x轴传播.T=0时的波形如图所示,质点A与质点B相距lm,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处.由此可知( )